|
Сотрудники :: Гасанов Эльяр Эльдарович :: Публикации Гасанова Э.Э.
Instantly solvable search problems
Eljar E. Gasanov
Moscow State University
ABSTRACT
This paper deals with the investigation of search time in database.
The search time is very important parameter for many information
systems (for example, the real-time systems).
Thus, the problem of construction of algorithms
minimizing the search time for the concrete information system is
very actual.
The new very fast on the average algorithms are suggested in the
paper. These algorithms solve some geometric search problems.
The estimations for the time complexity of these algorithms are
obtained.
KEYWORDS
Database theory; information search complexity; information
search modelling; fast algorithms.
INTRODUCTION
There are two approaches to construction of algorithms
solving information search problems.
The first approach supposes the creation of universal algorithms
having wide range of application. Usually this universality
leads to some loss of efficiency. The second approach
supposes the creation of effective algorithms but these
algorithms can be used in a narrow range.
Both approaches have a right to
existence. Usually the universal algorithms of organization and
search of data are used in the database systems, intended for
extensive commercial application. When the efficiency of the
universal algorithms do not satisfies in some special
databases then the necessity of construction of special data
organization and search algorithms appears. On the other
hand availability of the great number of effective algorithms,
which can be used in the various situations, can allow to realize
the third approach.
This approach consists in
the creation of an expert system, which can
help for each search problem to find suitable effective
algorithms from available ones in the expert system database.
Thus, the third approach unites advantages of the first and
second ones: on the one hand it can ensure applicability for a
wide class of problems but on the other hand it can ensure high
efficiency. Perspective of the third approach increases the
importance of effective algorithms construction in spite of
the narrowness of their application.
In this paper the search algorithms efficiency means the
average search time. The average search time is very important
parameter for all real-time systems. Therefore the problem of
construction of fast search algorithms is very actual.
Two new algorithms for solving two geometric search problems
are suggested in the paper.
These algorithms can be very useful for computer-aided design
and computer graphics systems.
Data is analysed and pre-processed before using
the data by search algorithm. These steps are doing
to achieve the optimal time of the search.
BASIC NOTIONS AND RESULTS
The following mathematical model of information
search problem is suggested in the paper .
Let 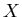 and and 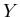 be some sets. Call be some sets. Call 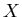 a set of queries
and a set of queries
and 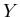 a set of objects to be found (or required objects).
Let a set of objects to be found (or required objects).
Let 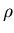 be a relation
on be a relation
on 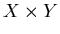 , which we call search relation. Say a
required object , which we call search relation. Say a
required object
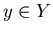 satisfies query satisfies query 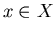 if if 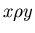 .
Let .
Let 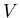 be some finite subset of be some finite subset of 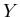 . .
Call triplet
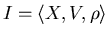 an information search problem (ISP).
ISP an information search problem (ISP).
ISP
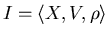 consists in enumeration for any query consists in enumeration for any query
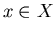 all that and only that objects all that and only that objects  , such that , such that
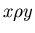 . .
Let
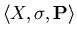 be a probability space
under be a probability space
under 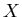 , where , where 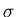 is the algebra of subsets of is the algebra of subsets of 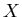 , ,
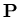 is probability measure on is probability measure on 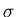 . .
Let 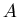 be some algorithm, which solves ISP be some algorithm, which solves ISP 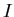 . .
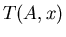 is solving time of is solving time of 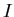 by by 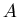 on query on query 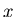 . .
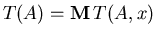 – average solving time of – average solving time of 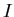 . .
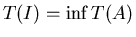 , where , where  is taken on the set of
all algorithms, solving problem is taken on the set of
all algorithms, solving problem  . .
A new mathematical model of the search algorithm was introduced
by the author (Gasanov, 1991). The notions of algorithm,
which solves ISP 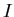 , and values , and values 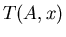 and and 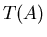 can be
formal defined in this model. But we do not describe this model
because the limit of space do not allow to do it. We notice
only that some schemes are corresponded to the search algorithms,
and these schemes are directed graphs. The required objects from can be
formal defined in this model. But we do not describe this model
because the limit of space do not allow to do it. We notice
only that some schemes are corresponded to the search algorithms,
and these schemes are directed graphs. The required objects from
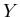 are corresponded to some nodes of this graph, and some
special functions are corresponded to edges or nodes of the
graph. The range of definition of these functions is the set of
queries X. The complexity of these schemes is defined so that
it reflects the average search time of correspondent algorithms. are corresponded to some nodes of this graph, and some
special functions are corresponded to edges or nodes of the
graph. The range of definition of these functions is the set of
queries X. The complexity of these schemes is defined so that
it reflects the average search time of correspondent algorithms.
Let
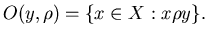
The following theorems are obtained.
Theorem 1
For any ISP
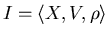
Say
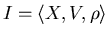 is an instantly solvable
search problem if
there exist algorithm is an instantly solvable
search problem if
there exist algorithm  , solving , solving 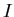 , such that , such that
where 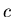 is a constant, independent of number of elements
of set V. is a constant, independent of number of elements
of set V.
Theorem 2
Let ![$X=(0,1]$](images/baden-baden/img26.gif) , ![$Y=(0,1]$](images/baden-baden/img27.gif) ,
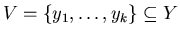 ,

Let for each 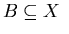
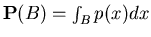 ,
where 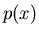 is
probability density function, and
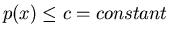 .
Then ISP
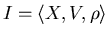 (which is
called problem of search of
identical objects) is instantly solvable search problem, and
Theorem 3
Let ![$Y={[0,1]}^n$](images/baden-baden/img35.gif) ,
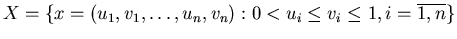 ,
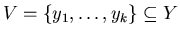 ,
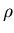 – relation on 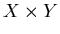
such that for
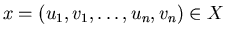 and
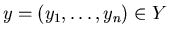
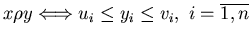 .
Let for each 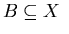
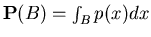 ,
where 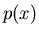 is
probability density function, and
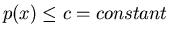 .
Then ISP
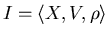 (which is called 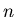 -dimensional
interval search problem)
is instantly solvable search problem, and
JUSTIFICATION OF THE RESULTS
Since we do not describe the mathematical model of the search
algorithms we cannot give the formal proof of the above theorems.
Therefore we give only the proof ideas and algorithms description.
The first theorem say that the average search time is not less
than the average time of the answer enumeration. It is the evident
and well known fact.
The result of the second theorem is founded on the following
search algorithm.
So
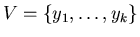 is our ordered set of the objects
to be found. is our ordered set of the objects
to be found.
Let
![$S_i=\left(\frac{i-1}{k},\frac{i}{k}\right]$](images/baden-baden/img43.gif) , ,
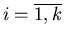 . .
Let
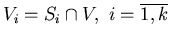 . .
Let ![$x\in (0,1]$](images/baden-baden/img46.gif) be some query. be some query.
On the first step we calculate the number ![$m=[x\cdot k]$](images/baden-baden/img47.gif) .
If .
If 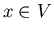 then then 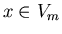 . Therefore on the second step
we do binary search in the set . Therefore on the second step
we do binary search in the set 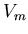 (if (if
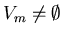 ).
The estimation of the theorem 2 is based on the fact that the
worst on the average situations is the case when ).
The estimation of the theorem 2 is based on the fact that the
worst on the average situations is the case when
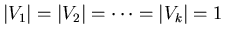 . The last fact follows from the
concavity of the logarithm function. . The last fact follows from the
concavity of the logarithm function.
When 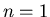 the result of the third theorem is grounded on
the following
search algorithm. the result of the third theorem is grounded on
the following
search algorithm.
Let
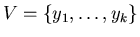 is our increasing ordered set of
the objects to be found. is our increasing ordered set of
the objects to be found.
Let
![$m=[2\,c\cdot \log k]$](images/baden-baden/img54.gif) . .
Let
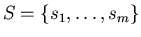 , where , where
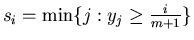 (if (if
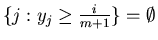 then then 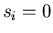 ). ).
Let 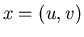 be some query from be some query from 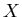 . .
On the first step we calculate the value 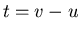 . .
If
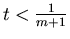 we find we find
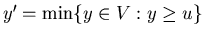 with the help of the binary search. Then we look through
the objects
with the help of the binary search. Then we look through
the objects  from left to right beginning from from left to right beginning from 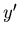 while
while 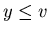 . .
If
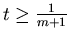 we calculate the value we calculate the value
![$p=[u\cdot (m+1)]$](images/baden-baden/img66.gif) . Obviously . Obviously
![$\frac{n}{m+1}\in [u,v]$](images/baden-baden/img67.gif) .
Therefore we will look through the objects .
Therefore we will look through the objects 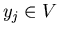 from left to right beginning from
from left to right beginning from 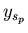 while while 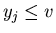 (we will do it only if
(we will do it only if 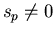 ).
Then we will look through the objects ).
Then we will look through the objects 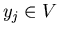 from
right to left beginning from from
right to left beginning from 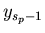 while while 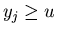 (if
(if 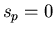 we will begin from we will begin from 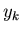 ). ).
Finally notice that
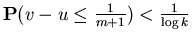 whence it follows the result of the
theorem 3 under condition whence it follows the result of the
theorem 3 under condition 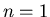 . .
The case 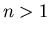 is proved by the method of dimension reduction. is proved by the method of dimension reduction.
CONCLUSION
The above-mentioned search problems are well known and widespread
geometric search problems. They are used in the all computer
graphics systems and CAD. For example, every time we are looking
for points located in some window we deal with the 2-dimensional
interval search problem.
The first above search problem is typical representative of problem
of search of identical objects, which occur in the all database
systems. Under certain conditions above algorithms can be used easily
for solving of the well known key search problem. Therefore the
results of this paper can be used in the large class of
information search systems when the search time is critical
parameter.
REFERENCE
Gasanov E.E. (1991); On one mathematical model of
information search;
Discrete mathematics, v. 3, No 2 (pp. 69-76) (in Russian).
Proceedings of International Symposium on Intelligent Data Analysis (IDA-95). Baden-Baden, Germany. HAS Press, 1995.
Наверх
|