|
Сотрудники :: Гасанов Эльяр Эльдарович :: Публикации Гасанова Э.Э.
Константный в худшем случае алгоритм поиска идентичных объектов
Гасанов Э.Э., Луговская Ю.П.
Московский государственный университет,
Российский государственный гуманитарный университет
Резюме:
В работе предлагается алгоритм поиска идентичных
объектов, который при затратах памяти порядка
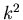
почти всегда обеспечивает время поиска в худшем случае в
6 элементарных операций,
здесь 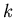 – мощность множества, в котором
производится поиск.
Оглавление
В работе рассматривается задача поиска идентичных
объектов в ее геометрической интерпретации, которая
звучит следующим образом. Дано конечное подмножество
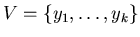 точек из отрезка точек из отрезка ![$[0,1]$](images/const/img4.gif) вещественной
прямой. Требуется построить условный алгоритм, который для
произвольной точки вещественной
прямой. Требуется построить условный алгоритм, который для
произвольной точки 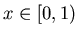 (эта точка называется запросом)
позволяет найти номер точки из множества (эта точка называется запросом)
позволяет найти номер точки из множества 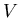 , которая
совпадает с , которая
совпадает с 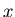 (если такая точка в (если такая точка в 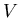 существует),
при условии, что мы умеем выполнять следующие операции
над вещественными числами: арифметические операции
(сложение, вычитание, умножение, деление, взятие
целой части вещественного числа), операции сравнения
и возможно некоторые другие простейшие операции.
При этом допускается предобработка данных, которая
может состоять в сортировке данных (множества существует),
при условии, что мы умеем выполнять следующие операции
над вещественными числами: арифметические операции
(сложение, вычитание, умножение, деление, взятие
целой части вещественного числа), операции сравнения
и возможно некоторые другие простейшие операции.
При этом допускается предобработка данных, которая
может состоять в сортировке данных (множества 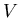 ),
а также в построении некоторых дополнительных структур.
Известным алгоритмом решения этой задачи является
алгоритм бинарного или дихотомического поиска
(см., например, [1, стр.484-492]). Здесь
и далее мы будем пользоваться термином "алгоритм",
подразумевая "условный алгоритм"
(или "относительный алгоритм", см. [2, с. 44-45]).
Известно, что время поиска бинарного алгоритма в
худшем случае и в среднем равно по порядку ),
а также в построении некоторых дополнительных структур.
Известным алгоритмом решения этой задачи является
алгоритм бинарного или дихотомического поиска
(см., например, [1, стр.484-492]). Здесь
и далее мы будем пользоваться термином "алгоритм",
подразумевая "условный алгоритм"
(или "относительный алгоритм", см. [2, с. 44-45]).
Известно, что время поиска бинарного алгоритма в
худшем случае и в среднем равно по порядку 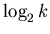 ,
а требуемый объем памяти по порядку равен ,
а требуемый объем памяти по порядку равен 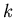 .
Здесь под временем поиска понимается количество
выполненных элементарных операций, под объемом памяти
количество ячеек для хранения вещественных чисел, куда
можно поместить данные и дополнительные
структуры, а худший случай и среднее берется по множеству
всех возможных значений запроса, т.е. по множеству .
Здесь под временем поиска понимается количество
выполненных элементарных операций, под объемом памяти
количество ячеек для хранения вещественных чисел, куда
можно поместить данные и дополнительные
структуры, а худший случай и среднее берется по множеству
всех возможных значений запроса, т.е. по множеству 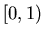 .
В [3] предлагается алгоритм с
затратами по памяти порядка .
В [3] предлагается алгоритм с
затратами по памяти порядка 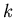 , в котором среднее
время поиска равно константе, но время поиска в худшем
случае имеет порядок , в котором среднее
время поиска равно константе, но время поиска в худшем
случае имеет порядок 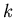 . В работах [4,5]
предложен алгоритм, который при объеме памяти порядка . В работах [4,5]
предложен алгоритм, который при объеме памяти порядка 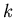 позволяет решать задачи в худшем случае за время порядка
позволяет решать задачи в худшем случае за время порядка
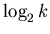 , а в среднем за 2 шага. В данной работе предлагается
алгоритм, который для почти всех задач поиска идентичных
объектов (т.е. при вариации множества , а в среднем за 2 шага. В данной работе предлагается
алгоритм, который для почти всех задач поиска идентичных
объектов (т.е. при вариации множества 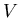 ) позволяет при
объеме памяти порядка ) позволяет при
объеме памяти порядка 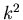 решать задачу в худшем
случае за 6 элементарных операций. решать задачу в худшем
случае за 6 элементарных операций.
Авторы выражают благодарность рецензенту
за ценные замечания.
Опишем предлагаемый алгоритм. Пусть нам дано множество
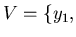
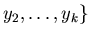 , в котором производится поиск.
Это множество будем называть библиотекой. Выполним
следующую предобработку. Упорядочим точки из , в котором производится поиск.
Это множество будем называть библиотекой. Выполним
следующую предобработку. Упорядочим точки из 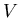 в порядке
возрастания и, чтобы не усложнять обозначения, далее
считаем, что в порядке
возрастания и, чтобы не усложнять обозначения, далее
считаем, что
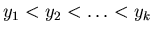 . Находим число . Находим число
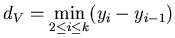 .
Пусть .
Пусть ![$m=]1/d_V[$](images/const/img14.gif) – наименьшее целое, не меньшее, чем – наименьшее целое, не меньшее, чем 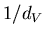 .
Выделим место под массив целых длины .
Выделим место под массив целых длины 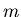 , и элементы этого
массива будем обозначать , и элементы этого
массива будем обозначать 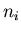 ( (
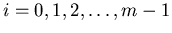 ).
Разделим отрезок ).
Разделим отрезок ![$[0,1]$](images/const/img4.gif) на на 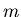 равных частей: равных частей:
![\begin{displaymath}A_i=[i/m,(i+1)/m),\ i=0,1,\ldots,m-2,\ A_{m-1}=[(m-1)/m,1].\end{displaymath}](images/const/img19.gif)
В каждую часть может попасть не более одной точки из множества
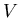 . Теперь заполним массив . Теперь заполним массив 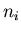 следующим образом: следующим образом:
![\begin{displaymath}
n_i = \left \{ \begin{array}{ll}
-1, & \mbox{\parbox[t]{8cm...
...точки из $V$, которая попала в
$A_i$,}}
\end{array} \right.
\end{displaymath}](images/const/img20.gif)
где
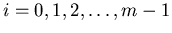 . .
После того как сделана данная предобработка, поиск будем
осуществлять следующим образом. Пусть нам дан запрос
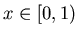 . Вычислим . Вычислим ![$j=[x\cdot m]$](images/const/img21.gif) – целая часть
числа – целая часть
числа 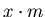 . Понятно, что . Понятно, что 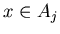 . Если . Если 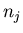 равно
равно 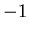 , то в библиотеке , то в библиотеке 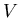 нет числа равного нет числа равного 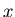 .
В противном случае сравниваем .
В противном случае сравниваем 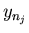 с с 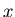 и если
они равны, то номер и если
они равны, то номер 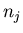 является ответом задачи,
иначе ответ пуст. Тем самым в худшем случае мы выполняем одну
операцию умножения, одну операцию взятия целой части,
одну операцию сравнения целых чисел,
одну операцию сравнения вещественных чисел и две
операции извлечения элемента массива, всего 6 операций.
Объем памяти, необходимый данному алгоритму, равен
сумме объемов массивов целых чисел длины является ответом задачи,
иначе ответ пуст. Тем самым в худшем случае мы выполняем одну
операцию умножения, одну операцию взятия целой части,
одну операцию сравнения целых чисел,
одну операцию сравнения вещественных чисел и две
операции извлечения элемента массива, всего 6 операций.
Объем памяти, необходимый данному алгоритму, равен
сумме объемов массивов целых чисел длины 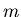 и
вещественных чисел длины и
вещественных чисел длины 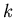 . Ниже приводятся
результаты, оценивающие величину . Ниже приводятся
результаты, оценивающие величину 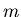 . .
Пусть
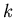 – натуральное число, большее 1 и – натуральное число, большее 1 и
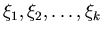 – независимые равномерно распределенные
на отрезке – независимые равномерно распределенные
на отрезке ![$[0,1]$](images/const/img4.gif) случайные величины.
Пусть случайные величины.
Пусть
Эта величина
исследовалась, например, в
[6] и [7].
Пусть
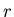 – вещественное число и – вещественное число и
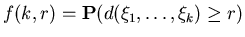 – вероятность того, что
минимальное расстояние между парами различных точек – вероятность того, что
минимальное расстояние между парами различных точек
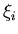 ( (
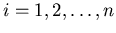 ) не меньше ) не меньше 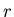 . .
Если считать, что библиотеки 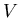 получаются
случайным независимым бросанием получаются
случайным независимым бросанием 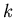 точек на отрезок точек на отрезок ![$[0,1]$](images/const/img4.gif) ,
где вероятность попадания в любые
два отрезка из ,
где вероятность попадания в любые
два отрезка из ![$[0,1]$](images/const/img4.gif) одинаковой длины
одинакова, то одинаковой длины
одинакова, то
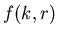 равна доле
множества равна доле
множества 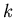 -элементных библиотек, у которых минимальное
расстояние между любыми двумя точками не меньше,
чем -элементных библиотек, у которых минимальное
расстояние между любыми двумя точками не меньше,
чем 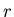 , по отношению к множеству всех библиотек
мощности , по отношению к множеству всех библиотек
мощности 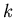 . .
Справедлива следующая теорема.
Чтобы привести следствие из этой теоремы, описывающее
асимптотическое поведение 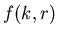 ,
введем обозначения, обычно принятые при описании
асимптотических оценок. ,
введем обозначения, обычно принятые при описании
асимптотических оценок.
Будем писать
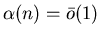 , если , если
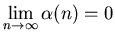 . .
Будем писать
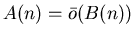 , если , если
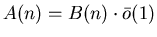 . .
Скажем, что 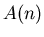 асимптотически не превосходит асимптотически не превосходит 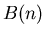 при при
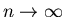 и обозначим и обозначим
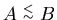 , если существует , если существует
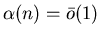 такое, что начиная с некоторого
номера такое, что начиная с некоторого
номера 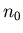 , ,
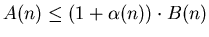 . .
Если
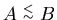 и и
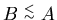 ,
то будем говорить, что ,
то будем говорить, что 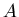 и и 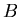 асимптотически равны при асимптотически равны при
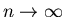 и обозначать и обозначать 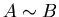 . .
Будем писать
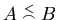 , если существует
такая положительная константа , если существует
такая положительная константа 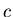 , что, начиная с некоторого
номера , что, начиная с некоторого
номера 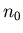 , ,
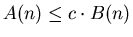 . .
Если
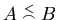 и и
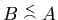 ,
то будем говорить, что ,
то будем говорить, что 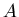 и и 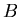 равны по порядку при равны по порядку при
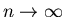 . .
Теорема 2
Пусть 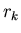 – последовательность
вещественных чисел, такая, что
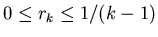 .
Тогда
Отсюда следует, что если в нашем распоряжении имеется
объем памяти размера 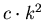 , то доля библиотек
мощности , то доля библиотек
мощности 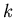 , для которых описанным алгоритмом мы
можем находить ответ за 6 элементарных операций, равна , для которых описанным алгоритмом мы
можем находить ответ за 6 элементарных операций, равна
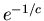 . А если в нашем распоряжении имеется объем памяти
больший по порядку, чем . А если в нашем распоряжении имеется объем памяти
больший по порядку, чем 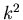 , то для почти всех библиотек
мы можем находить ответ за 6 шагов. С другой стороны,
если у нас имеется объем памяти, меньший по порядку, чем , то для почти всех библиотек
мы можем находить ответ за 6 шагов. С другой стороны,
если у нас имеется объем памяти, меньший по порядку, чем
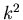 , то почти всегда мы не сможем воспользоваться
описанным выше алгоритмом поиска. , то почти всегда мы не сможем воспользоваться
описанным выше алгоритмом поиска.
Обозначим через
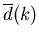 среднее значение
описанной выше величины среднее значение
описанной выше величины
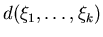 ,
тогда справедливо следующее утверждение. ,
тогда справедливо следующее утверждение.
Теорема 3
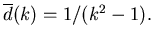
Отсюда следует, что в "среднем" достаточно
иметь 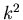 памяти, чтобы обеспечить время поиска в
6 операций. памяти, чтобы обеспечить время поиска в
6 операций.
Доказательство теоремы 1.
Пусть
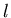 – вещественное число из отрезка – вещественное число из отрезка ![$[0,1]$](images/const/img4.gif) , ,
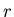 – вещественное число, – вещественное число,
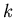 – натуральное число, большее 1, – натуральное число, большее 1,
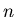 – такое натуральное число, что – такое натуральное число, что 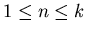 .
Пусть .
Пусть
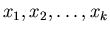 – независимые равномерно распределенные
на отрезке – независимые равномерно распределенные
на отрезке ![$[0,1]$](images/const/img4.gif) случайные величины.
Обозначим через случайные величины.
Обозначим через 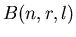 событие, что
точки событие, что
точки
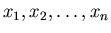 попадают в отрезок попадают в отрезок ![$[0,l]$](images/const/img67.gif) , и
минимальное расстояние между парами различных точек , и
минимальное расстояние между парами различных точек
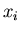 ( (
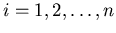 ),
не меньше ),
не меньше 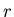 .
Обозначим через .
Обозначим через
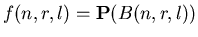 .
Понятно, что если .
Понятно, что если 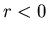 , то , то 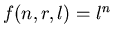 , а
при , а
при 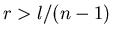 , , 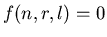 .
Поэтому мы будем рассматривать только случай, когда .
Поэтому мы будем рассматривать только случай, когда
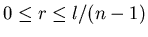 . .
Лемма 1
Если
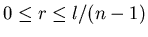 , то
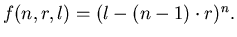
Доказательство будем вести индукцией по 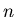 . .
Базис индукции. 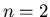 . .
Поскольку возможны два равновероятных события: случай
когда 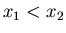 , и когда , и когда 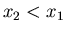 , то достаточно рассмотреть
первую ситуацию и удвоить полученный результат. Поскольку в
этом случае , то достаточно рассмотреть
первую ситуацию и удвоить полученный результат. Поскольку в
этом случае 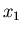 может меняться от 0 до может меняться от 0 до 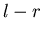 , а , а 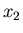 –
от –
от 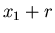 до до 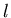 , то , то
Индуктивный переход. Пусть утверждение
леммы справедливо для любого натурального 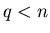 и любого вещественного
и любого вещественного ![$l\in [0,1]$](images/const/img85.gif) . .
Через 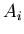 обозначим событие, что случайная величина обозначим событие, что случайная величина 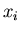 ,
максимальна среди величин ,
максимальна среди величин
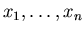 , здесь , здесь 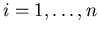 .
Понятно, что если .
Понятно, что если
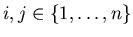 и и 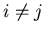 , то , то
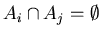 , кроме того , кроме того
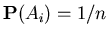 , для любого , для любого
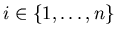 .
Легко
видеть, что .
Легко
видеть, что
Поскольку в случае события
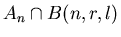 величина
величина 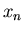 может меняться от может меняться от 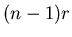 до до 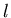 , а
остальные , а
остальные 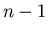 величины располагаются на отрезке величины располагаются на отрезке
![$[0,x_n-r]$](images/const/img99.gif) и должны находиться на расстоянии не менее и должны находиться на расстоянии не менее
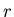 , то согласно предположению индукции , то согласно предположению индукции
Тем самым лемма доказана.
Чтобы убедиться в справедливости утверждения
теоремы 1 достаточно заметить,
что
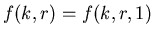 . .
Доказательство теоремы 2.
Пусть
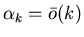 при при
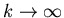 .
Воспользовавшись вторым
замечательным пределом, легко получить .
Воспользовавшись вторым
замечательным пределом, легко получить
Рассмотрим случай, когда
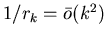 при
при
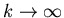 . .
Это означает, что для некоторой последовательности
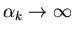 при при
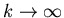 выполняется
выполняется
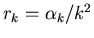 .
Поскольку .
Поскольку
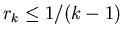 , то достаточно рассмотреть
два подслучая: , то достаточно рассмотреть
два подслучая:
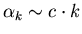 , где , где 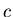 –
константа не превышающая 1, и –
константа не превышающая 1, и
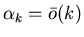 .
В первом подслучае .
В первом подслучае
Так как во втором подслучае
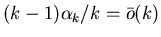 ,
то согласно (1) ,
то согласно (1)
Рассмотрим случай, когда
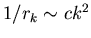 при
при
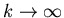 , где , где 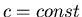 . .
Поскольку
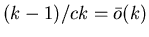 ,
то согласно (1) ,
то согласно (1)
И наконец, рассмотрим случай, когда
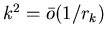 при
при
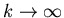 . .
Это означает, что для некоторой последовательности
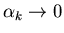 при при
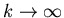 выполняется
выполняется
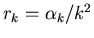 .
Поскольку .
Поскольку
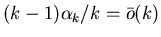 ,
то согласно (1) ,
то согласно (1)
Тем самым теорема 2 доказана.
Доказательство теоремы 3.
Обозначим через 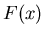 функцию распределения случайной
величины функцию распределения случайной
величины
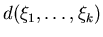 . .
Тогда так как при 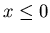 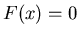 , а при , а при 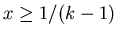
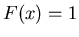 , то используя формулу интегрирования по частям,
нетрудно получить , то используя формулу интегрирования по частям,
нетрудно получить
Тем самым теорема 3 доказана.
- 1
-
Кнут Д. Искусство программирования для ЭВМ.
Сортировка и поиск. 3, Мир, Москва, 1978.
- 2
-
Мальцев А. И. Алгоритмы и рекурсивные функции. Наука,
Москва, 1986.
- 3
-
Ершов А. П. О программировании
арифметических операторов. ДАН СССР (1958) 118, 427-430.
- 4
-
Гасанов Э. Э. Мгновенно решаемые задачи поиска.
Дискретная математика (1996) 8, 3, 119-134.
- 5
-
Гасанов Э. Э. Функционально-сетевые базы
данных и сверхбыстрые алгоритмы поиска.
Изд. центр РГГУ, Москва, 1997.
- 6
-
Devroye L. Upper and lower class sequences for minimal
uniform spacings. Zeitschrift für
Wahrscheinlichkeitstheorie und verwande Gebiete (1982)
61, 2, 237-254.
- 7
-
Дейвид Г. Порядковые статистики.
Наука, Москва, 1979, с. 119.
Работа выполнена при финансовой поддержке
Российского фонда фундаментальных исследований
(грант 98-01-00130)
Оглавление
Дискретная математика (1999) 11, N 4,
Наверх
|