|
Сотрудники :: Гасанов Эльяр Эльдарович :: Публикации Гасанова Э.Э.
Решение
проблемы оптимального синтеза
информационных графов
для базовых задач поиска информации
Гасанов Э.Э.
Кафедра математической теории интеллектуальных систем,
механико-математический факультет МГУ им М.В.Ломоносова
0. Построена новая общая модель
хранения и поиска информации, называемая информационно-графовой,
частными случаями которой являются известные базовые примеры
такого рода. Изучены основные свойства этой модели и решена
проблема оптимального синтеза информационных графов для широкого
класса задач поиска, включающего базовые примеры. Более полная
версия излагаемых результатов содержится в [1].
1. Пусть 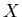 – множество запросов с заданным на нем
вероятностным пространством – множество запросов с заданным на нем
вероятностным пространством
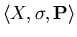 , где , где 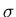 – алгебра
подмножеств множества – алгебра
подмножеств множества 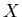 , , 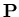 – вероятностная мера на – вероятностная мера на 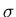 ; ;
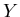 – множество записей (объектов поиска); – множество записей (объектов поиска);
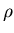 – бинарное отношение на – бинарное отношение на 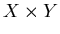 , называемое отношением
поиска;
пятерку , называемое отношением
поиска;
пятерку
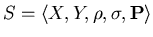 будем называть типом;
тройку
будем называть типом;
тройку
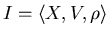 , где , где
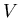 – некоторое
конечное подмножество множества – некоторое
конечное подмножество множества 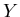 ,
будем называть задачей информационного поиска (ЗИП)
типа ,
будем называть задачей информационного поиска (ЗИП)
типа 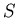 , и
будем считать, что ЗИП , и
будем считать, что ЗИП
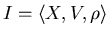 содержательно состоит в перечислении для
произвольно взятого запроса
содержательно состоит в перечислении для
произвольно взятого запроса
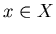 всех тех и только тех записей всех тех и только тех записей  , таких
что , таких
что 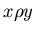 ; ;
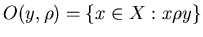 ;
если ;
если
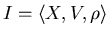 , то , то
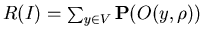 ;
если ;
если
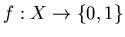 ,
то ,
то
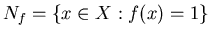 ; ;
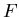 – множество символов одноместных предикатов, определенных
на множестве – множество символов одноместных предикатов, определенных
на множестве 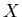 ; ;
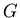 – множество символов одноместных переключателей,
определенных на множестве – множество символов одноместных переключателей,
определенных на множестве 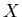 ,
под переключателями будем понимать
функции, областью значений которых являются конечные подмножества
натурального ряда;
пару ,
под переключателями будем понимать
функции, областью значений которых являются конечные подмножества
натурального ряда;
пару
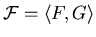 назовем базовым множеством; назовем базовым множеством;
Понятие информационного графа
(ИГ) над базовым множеством
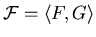 ,
определяется следующим образом.
Берется конечная
многополюсная ориентированная сеть. В ней выбирается
некоторый полюс, который называется корнем.
Остальные полюса называются
листьями и им приписываются
записи из ,
определяется следующим образом.
Берется конечная
многополюсная ориентированная сеть. В ней выбирается
некоторый полюс, который называется корнем.
Остальные полюса называются
листьями и им приписываются
записи из 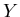 , причем
разным листьям могут быть приписаны одинаковые записи. Некоторые
вершины сети (в том числе это могут быть и полюса) называются
переключательными и им приписываются переключатели из , причем
разным листьям могут быть приписаны одинаковые записи. Некоторые
вершины сети (в том числе это могут быть и полюса) называются
переключательными и им приписываются переключатели из 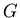 .
Ребра, исходящие из каждой из переключательных вершин,
нумеруются начиная с 1 и называются переключательными ребрами.
Ребра, не являющиеся переключательными,
называются предикатными и им приписываются предикаты из множества .
Ребра, исходящие из каждой из переключательных вершин,
нумеруются начиная с 1 и называются переключательными ребрами.
Ребра, не являющиеся переключательными,
называются предикатными и им приписываются предикаты из множества
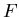 .
Таким образом нагруженную многополюсную ориентированную
сеть называем ИГ над базовым множеством .
Таким образом нагруженную многополюсную ориентированную
сеть называем ИГ над базовым множеством
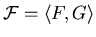 . .
Функционирование ИГ определяется следующим образом.
Скажем, что: предикатное ребро проводит запрос 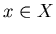 ,
если предикат, приписанный этому ребру, принимает значение
1 на запросе ,
если предикат, приписанный этому ребру, принимает значение
1 на запросе 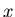 ;
переключательное ребро, которому приписан номер ;
переключательное ребро, которому приписан номер 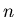 ,
проводит запрос ,
проводит запрос 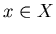 ,
если переключатель, приписанный началу этого ребра, принимает значение ,
если переключатель, приписанный началу этого ребра, принимает значение
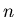 на запросе на запросе 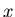 ;
ориентированная цепочка ребер
проводит запрос ;
ориентированная цепочка ребер
проводит запрос 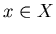 ,
если каждое ребро цепочки
проводит запрос ,
если каждое ребро цепочки
проводит запрос 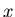 ;
запрос ;
запрос 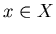 проходит в вершину проходит в вершину 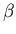 ИГ,
если существует ориентированная цепочка, ведущая из
корня в вершину ИГ,
если существует ориентированная цепочка, ведущая из
корня в вершину 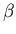 , которая проводит запрос , которая проводит запрос 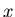 ;
запись ;
запись 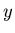 , приписанная листу , приписанная листу 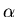 ,
попадает в ответ ИГ на запрос ,
попадает в ответ ИГ на запрос 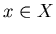 , если
запрос , если
запрос 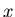 проходит в лист проходит в лист 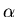 .
Ответом ИГ .
Ответом ИГ 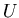 на запрос на запрос 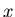 назовем множество
записей, попавших в ответ ИГ на запрос назовем множество
записей, попавших в ответ ИГ на запрос 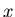 , и
обозначим его , и
обозначим его 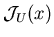 .
Эту функцию .
Эту функцию 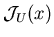 будем считать
результатом функционирования ИГ будем считать
результатом функционирования ИГ 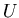 . .
Пусть нам дана ЗИП
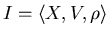 .
Скажем, что ИГ .
Скажем, что ИГ 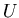 разрешает ЗИП разрешает ЗИП
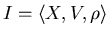 ,
если ,
если
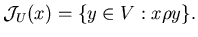
Введем понятие сложности ИГ.
Пусть 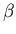 – некоторая вершина ИГ.
Предикат, определенный на множестве запросов, который
принимает значение 1 на запросе – некоторая вершина ИГ.
Предикат, определенный на множестве запросов, который
принимает значение 1 на запросе 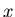 , если
запрос проходит в вершину , если
запрос проходит в вершину 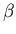 , и 0 – в противном
случае, назовем функцией фильтра вершины , и 0 – в противном
случае, назовем функцией фильтра вершины 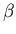 и
обозначим и
обозначим
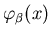 . .
Сложностью ИГ 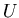 на запросе на запросе 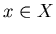 назовем число назовем число
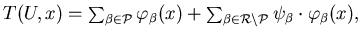 где
где 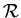 – множество вершин ИГ – множество вершин ИГ 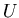 , ,
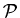 – множество переключательных вершин ИГ – множество переключательных вершин ИГ 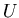 , ,
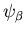 – количество ребер, исходящих из
вершины – количество ребер, исходящих из
вершины 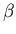 . .
Скажем, что базовое множество 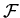 измеримое,
если каждая функция из
измеримое,
если каждая функция из 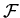 – измеримая
(относительно алгебры – измеримая
(относительно алгебры 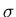 ).
Далее всюду будем предполагать, что
базовое множество измеримое.
В этом случае для
любого ИГ ).
Далее всюду будем предполагать, что
базовое множество измеримое.
В этом случае для
любого ИГ 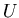 над над
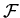 функция функция 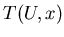 как функция от
как функция от 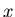 измерима. измерима.
Сложностью ИГ 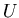 назовем математическое ожидание величины назовем математическое ожидание величины
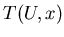 , то есть число
Сложностью задачи , то есть число
Сложностью задачи 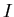 при
базовом множестве
при
базовом множестве 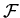 назовем число назовем число
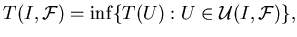 где
где
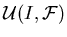 – множество всех ИГ над базовым
множеством – множество всех ИГ над базовым
множеством 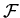 , разрешающих ЗИП , разрешающих ЗИП 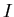 . .
2.
Задача поиска идентичных объектов
состоит в
поиске в множестве объекта, идентичного объекту-запросу,
и формально принадлежит типу
![$ {S_{id}}=\langle [0,1], [0,1], = ,\sigma,{\bf P} \rangle$](images/danrossii/img41.gif) .
Задачи о близости
состоят в поиске в линейно-упорядоченном множестве
объекта, ближайшего к объекту-запросу,
и принадлежат типу: .
Задачи о близости
состоят в поиске в линейно-упорядоченном множестве
объекта, ближайшего к объекту-запросу,
и принадлежат типу:
![$ {S_{ne}}=\langle [0,1], [0,1],{\rho_{ne}},\sigma,{\bf P} \rangle,$](images/danrossii/img42.gif) где
где 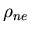 задается на задается на ![$[0,1]\times V$](images/danrossii/img44.gif) и определяется
соотношением и определяется
соотношением
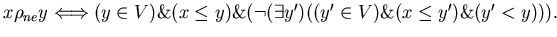 Справедлива теорема
[2].
Справедлива теорема
[2].
Теорема 1
Пусть 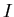 – ЗИП типа 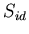 или
типа 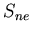 ,
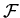 – базовое множество,
содержащее арифметические операции и
операции сравнения.
Тогда
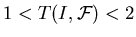 .
Задача включающего поиска
принадлежит следующему типу:
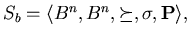 где
где 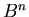 – единичный – единичный 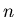 -мерный куб, -мерный куб,
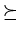 – отношение частичного порядка на – отношение частичного порядка на 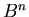 "не меньше
по-компонентно", "не меньше
по-компонентно", 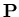 –
равномерная вероятностная мера на –
равномерная вероятностная мера на 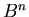 .
Справедлива теорема
[3]. .
Справедлива теорема
[3].
Теорема 2
Пусть базовое множество имеет вид
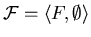 ,
где
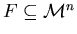 и
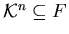 , и
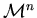 –
множество монотонных булевых функций,
а 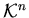 –
множество элементарных монотонных конъюнкций.
Тогда
для любой ЗИП 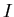 типа 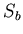
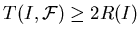
и существуют такие ЗИП
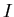 типа 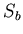 ,
что
при
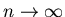
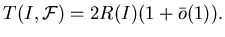
Задача о доминировании
состоит в
поиске в конечном подмножестве 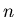 -мерного пространства всех
тех точек, которые не больше по каждой из компонент чем
запрос, являющийся в данном случае точкой -мерного пространства всех
тех точек, которые не больше по каждой из компонент чем
запрос, являющийся в данном случае точкой 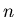 -мерного пространства.
Пусть -мерного пространства.
Пусть
![${X_n}={[0,1]}^n$](images/danrossii/img61.gif) .
Отношение поиска .
Отношение поиска 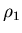 определено на определено на
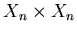 и задается
следующим соотношением: и задается
следующим соотношением:
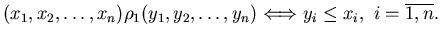 Тогда тип
Тогда тип
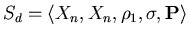 назовем типом задачи о доминировании.
Задача интервального поиска
состоит в
поиске в конечном подмножестве
назовем типом задачи о доминировании.
Задача интервального поиска
состоит в
поиске в конечном подмножестве 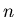 -мерного пространства всех
тех точек, которые попадают в -мерного пространства всех
тех точек, которые попадают в 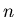 -мерный параллелепипед-запрос.
Пусть -мерный параллелепипед-запрос.
Пусть
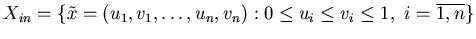 .
Отношение поиска .
Отношение поиска 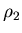 определено на определено на
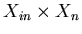 и задается
следующим соотношением: и задается
следующим соотношением:
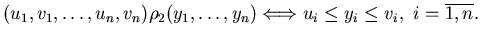 Тогда тип
Тогда тип
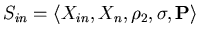 назовем типом интервального поиска.
Справедлива следующая теорема
[2,4].
назовем типом интервального поиска.
Справедлива следующая теорема
[2,4].
Теорема 3
Пусть 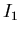
– ЗИП типа 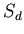 ,
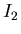
– ЗИП типа 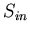 ,
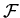 – базовое множество,
содержащее арифметические операции и
операции сравнения.
Тогда
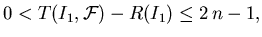
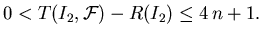
- 1
-
Гасанов Э. Э. Информационно-графовая модель
хранения и поиска данных.
Интеллектуальные системы (1998) 3, 3-4,
163-192.
- 2
-
Гасанов Э. Э. Мгновенно решаемые задачи поиска.
Дискретная математика (1996) 8, 3, 119-134.
- 3
-
Гасанов Э. Э. Нижняя оценка сложности информационных сетей
для одного отношения частичного порядка.
Дискретная математика (1996) 8, 4, 108-122.
- 4
-
Гасанов Э. Э. Функционально-сетевые базы
данных и сверхбыстрые алгоритмы поиска.
Изд. центр РГГУ, Москва, 1997.
1
Работа выполнена при финансовой поддержке
Российского фонда фундаментальных исследований
(грант 98-01-00130)
ДАН (2000) 374, N 4.
Наверх
|