|
Сотрудники :: Гасанов Эльяр Эльдарович :: Публикации Гасанова Э.Э.
Информационно-графовая модель данных с нечеткой логикой
Гасанов Э.Э., Фещук А.А.
Кафедра математической теории интеллектуальных систем,
механико-математический факультет МГУ им М.В.Ломоносова
Резюме:
Предлагается математическая модель для описания информационного
поиска с нечеткой логикой. Приводятся простейшие свойства
модели, такие как критерий допустимости информационного графа и
критерий полноты базового множества. Описывается некоторый метод
перехода от четкой задачи поиска к нечеткой и приводятся условия,
при которых решение четкой задачи будет решением соответствующей
нечеткой.
В соответствии с [1] введем понятие задачи
информационного поиска.
Пусть 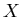 – множество запросов; – множество запросов;
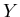 – множество записей (объектов поиска); – множество записей (объектов поиска);
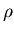 – бинарное отношение на – бинарное отношение на 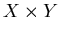 , называемое
отношением поиска;
тройку , называемое
отношением поиска;
тройку
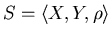 будем называть типом;
тройку
будем называть типом;
тройку
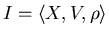 , где , где
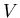 – некоторое
конечное подмножество множества – некоторое
конечное подмножество множества 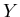 ,
будем называть задачей информационного поиска (ЗИП)
типа ,
будем называть задачей информационного поиска (ЗИП)
типа 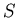 , и
будем считать, что ЗИП , и
будем считать, что ЗИП
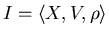 содержательно состоит в перечислении для
произвольно взятого запроса
содержательно состоит в перечислении для
произвольно взятого запроса
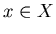 всех тех и только тех записей всех тех и только тех записей  , таких
что , таких
что 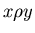 . .
По аналогии с этим определением введем понятие задачи
нечеткого поиска. Пусть как и ранее
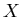 – множество запросов, – множество запросов,
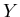 – множество записей.
Пусть задано отображение – множество записей.
Пусть задано отображение
![$\eta(x,y): X \times Y \rightarrow [0,1]$](images/igmd/img12.gif) ,
которое будем называть
отношением нечеткого поиска.
Тройку ,
которое будем называть
отношением нечеткого поиска.
Тройку
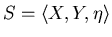 будем называть типом нечеткого поиска;
тройку
будем называть типом нечеткого поиска;
тройку
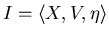 , где , где
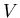 – некоторое
конечное подмножество множества – некоторое
конечное подмножество множества 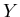 ,
будем называть задачей нечеткого поиска (ЗНП)
типа ,
будем называть задачей нечеткого поиска (ЗНП)
типа 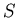 , и
будем считать, что ЗНП , и
будем считать, что ЗНП
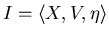 содержательно состоит в том, чтобы
для произвольного числа
содержательно состоит в том, чтобы
для произвольного числа ![$c\in [0,1]$](images/igmd/img15.gif) и
произвольного запроса и
произвольного запроса
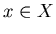 перечислить все те и только те записи перечислить все те и только те записи  , такие
что , такие
что
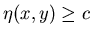 . .
Введем несколько упрощенное по сравнению с [1] понятие
информационного графа.
Пусть 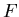 – множество символов одноместных предикатов, определенных
на множестве – множество символов одноместных предикатов, определенных
на множестве 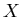 , называемое базовым множеством. , называемое базовым множеством.
Понятие информационного графа
(ИГ) над базовым множеством
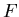 ,
определяется следующим образом.
Берется конечная
многополюсная ориентированная сеть. В ней выбирается
некоторый полюс, который называется корнем.
Остальные полюса называются
листьями и им приписываются
записи из ,
определяется следующим образом.
Берется конечная
многополюсная ориентированная сеть. В ней выбирается
некоторый полюс, который называется корнем.
Остальные полюса называются
листьями и им приписываются
записи из 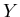 , причем
разным листьям могут быть приписаны одинаковые записи.
Ребрам
приписываются предикаты из множества , причем
разным листьям могут быть приписаны одинаковые записи.
Ребрам
приписываются предикаты из множества
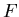 .
Таким образом нагруженную многополюсную ориентированную
сеть называем ИГ над базовым множеством .
Таким образом нагруженную многополюсную ориентированную
сеть называем ИГ над базовым множеством 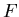 . .
Функционирование ИГ определяется следующим образом.
Скажем, что: ребро проводит запрос 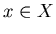 ,
если предикат, приписанный этому ребру, принимает значение
1 на запросе ,
если предикат, приписанный этому ребру, принимает значение
1 на запросе 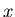 ;
ориентированная цепочка ребер
проводит запрос ;
ориентированная цепочка ребер
проводит запрос 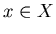 ,
если каждое ребро цепочки
проводит запрос ,
если каждое ребро цепочки
проводит запрос 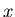 ;
запрос ;
запрос 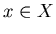 проходит в вершину проходит в вершину 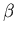 ИГ,
если существует ориентированная цепочка, ведущая из
корня в вершину ИГ,
если существует ориентированная цепочка, ведущая из
корня в вершину 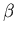 , которая проводит запрос , которая проводит запрос 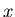 ;
запись ;
запись 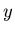 , приписанная листу , приписанная листу 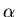 ,
попадает в ответ ИГ на запрос ,
попадает в ответ ИГ на запрос 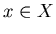 , если
запрос , если
запрос 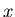 проходит в лист проходит в лист 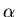 .
Ответом ИГ .
Ответом ИГ 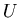 на запрос на запрос 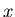 назовем множество
записей, попавших в ответ ИГ на запрос назовем множество
записей, попавших в ответ ИГ на запрос 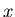 , и
обозначим его , и
обозначим его 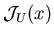 .
Эту функцию .
Эту функцию 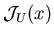 будем считать
результатом функционирования ИГ будем считать
результатом функционирования ИГ 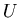 . .
Пусть нам дана ЗИП
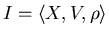 .
Скажем, что ИГ .
Скажем, что ИГ 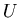 допустим для ЗИП допустим для ЗИП
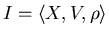 ,
если ,
если
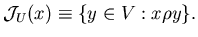
Множество ИГ над базовым множеством 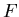 ,
допустимых для ЗИП ,
допустимых для ЗИП 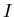 , обозначим , обозначим 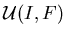 . .
Аналогично введем понятие нечеткого информационного графа.
Пусть
![${\cal F}= \{ f_a\vert f_a:X\rightarrow [0,1], a\in A \} $](images/igmd/img27.gif) –
базовое множество нечетких функций на –
базовое множество нечетких функций на 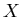 , где , где
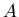 – некоторое множество индексов. – некоторое множество индексов.
Понятие нечеткого информационного графа
(НИГ) над базовым множеством
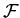 ,
определяется следующим образом.
Берется конечная
многополюсная ориентированная сеть. В ней выбирается
некоторый полюс, который называется корнем.
Остальные полюса называются
листьями и им приписываются
записи из ,
определяется следующим образом.
Берется конечная
многополюсная ориентированная сеть. В ней выбирается
некоторый полюс, который называется корнем.
Остальные полюса называются
листьями и им приписываются
записи из 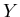 , причем
разным листьям могут быть приписаны одинаковые записи.
Ребрам
приписываются функции
из множества , причем
разным листьям могут быть приписаны одинаковые записи.
Ребрам
приписываются функции
из множества
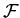 .
Таким образом нагруженную многополюсную ориентированную
сеть называем НИГ над базовым множеством .
Таким образом нагруженную многополюсную ориентированную
сеть называем НИГ над базовым множеством 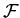 . .
Функционирование НИГ определяется следующим образом.
Проводимостью ребра НИГ назовем функцию,
равную функции, приписанной этому ребру;
проводимостью ориентированной цепочки ребер НИГ
назовем функцию, равную минимуму проводимостей ребер
цепочки; функцией фильтра вершины 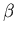 НИГ
(обозначается НИГ
(обозначается
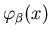 ),
назовем функцию равную максимуму функций проводимости
ориентированных цепочек, ведущих из корня НИГ в
вершину ),
назовем функцию равную максимуму функций проводимости
ориентированных цепочек, ведущих из корня НИГ в
вершину 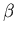 ;
скажем, что запись ;
скажем, что запись 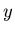 , приписанная листу , приписанная листу 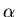 ,
попадает в ответ НИГ на запрос ,
попадает в ответ НИГ на запрос 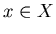 для числа для числа
![$c\in [0,1]$](images/igmd/img15.gif) , если , если
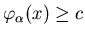 .
Ответом НИГ .
Ответом НИГ 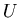 на запрос на запрос 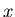 для числа для числа
![$c\in [0,1]$](images/igmd/img15.gif) назовем множество
записей, попавших в ответ НИГ на запрос назовем множество
записей, попавших в ответ НИГ на запрос 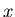 для числа
для числа
![$c\in [0,1]$](images/igmd/img15.gif) , и
обозначим его , и
обозначим его
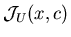 .
Эту функцию .
Эту функцию
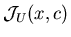 будем считать
результатом функционирования НИГ будем считать
результатом функционирования НИГ 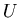 . .
Скажем, что НИГ 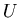 допустим для ЗНП допустим для ЗНП
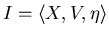 , если
для любого запроса , если
для любого запроса 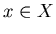 и любого числа и любого числа ![$c\in [0,1]$](images/igmd/img15.gif) выполняется
выполняется
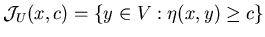 . .
Множество НИГ над базовым множеством 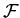 ,
допустимых для ЗНП ,
допустимых для ЗНП 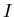 , обозначим , обозначим
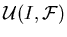 . .
Если 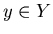 , то множество , то множество
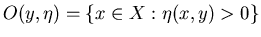 назовем тенью записи
назовем тенью записи 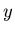 . .
Пусть 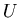 – некоторый НИГ, – некоторый НИГ, 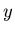 – запись из – запись из 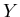 . Через . Через 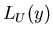 обозначим множество листьев НИГ
обозначим множество листьев НИГ 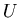 , которым соответствует
запись , которым соответствует
запись 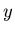 . .
Справедлива следующая теорема.
Базовое множество 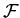 называется полным для
типа называется полным для
типа
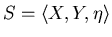 , если для любой ЗНП , если для любой ЗНП
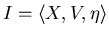 типа типа 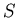 существует НИГ
существует НИГ 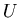 над базовым множеством над базовым множеством 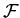 ,
допустимый для ЗНП ,
допустимый для ЗНП 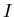 . .
Справедлив следующий результат, относящийся к проблеме
полноты для НИГ.
Теорема 2
Базовое множество 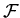 будет
полным для типа
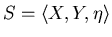
тогда и только тогда, когда
для любой записи 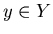 такой, что
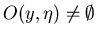 ,
функция 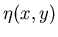 как функция от 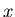
может быть представлена формулой вида
где
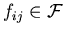 .
Теоремы 1 и 2
доказываются аналогично теоремам
1 и 2 из
[2].
Введем некоторый способ перехода от задачи информационного
поиска к задаче нечеткого поиска, такой, что для числа
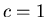 задача нечеткого поиска совпадает с исходной
задачей информационного поиска. задача нечеткого поиска совпадает с исходной
задачей информационного поиска.
Далее всюду будем считать, что
множество запросов ![$X=[0,1]$](images/igmd/img49.gif) и записей и записей ![$Y=[0,1]$](images/igmd/img50.gif) . .
Рассмотрим некоторую функцию
![$\mu:\mbox{$\mbox{\msbm R}$}^2 \rightarrow [0,1]$](images/igmd/img51.gif) ,
такую, что ,
такую, что
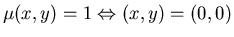 и и
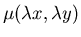 – невозрастающая функция от – невозрастающая функция от 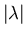 при
фиксированном при
фиксированном 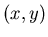 .
Рассмотрим некоторую функцию .
Рассмотрим некоторую функцию
![$\mu':\mbox{$\mbox{\msbm R}$}\rightarrow [0,1]$](images/igmd/img56.gif) ,
такую, что ,
такую, что
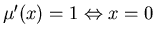 и и
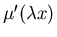 – невозрастающая функция от – невозрастающая функция от 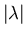 .
Пару .
Пару
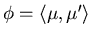 назовем основанием перехода.
Основание назовем основанием перехода.
Основание
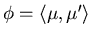 позволяет задать оператор перехода
позволяет задать оператор перехода 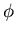 , который
каждой ЗИП позволяет сопоставить
некоторую ЗНП, а каждому ИГ некоторый НИГ. , который
каждой ЗИП позволяет сопоставить
некоторую ЗНП, а каждому ИГ некоторый НИГ.
Пусть
![$\rho\subseteq[0,1]^2$](images/igmd/img61.gif) – отношение поиска.
Через – отношение поиска.
Через 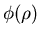 обозначим нечеткое отношение обозначим нечеткое отношение
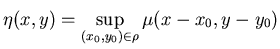
Каждой ЗИП
![$I=\langle [0,1],V,\rho\rangle$](images/igmd/img64.gif) сопоставим ЗНП
сопоставим ЗНП
![$\phi(I)=\langle [0,1],V,\phi(\rho)\rangle$](images/igmd/img65.gif) . .
Пусть 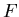 – некоторое базовое множество предикатов на – некоторое базовое множество предикатов на ![$[0,1]$](images/igmd/img66.gif) .
Если .
Если 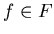 , то обозначим , то обозначим
![$N_f =\{x\in [0,1]:f(x)=1\}$](images/igmd/img68.gif) .
Если .
Если
![$A\subseteq [0,1]$](images/igmd/img69.gif) , то обозначим , то обозначим
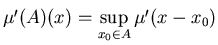 .
Предикату .
Предикату 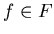 сопоставим функцию сопоставим функцию
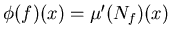 .
Множеству .
Множеству 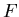 сопоставим базовое множество нечетких функций сопоставим базовое множество нечетких функций
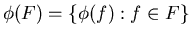 . .
Пусть 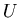 – ИГ над базовым множеством – ИГ над базовым множеством
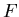 . Сопоставим ему НИГ . Сопоставим ему НИГ 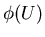 над базовым множеством над базовым множеством
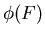 , полученный из ИГ , полученный из ИГ 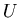 заменой для каждого ребра ИГ заменой для каждого ребра ИГ 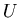 предиката
предиката 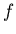 , приписанного этому ребру, на функцию , приписанного этому ребру, на функцию 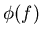 . .
Скажем, что базовое множество предикатов 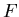 и основание
и основание
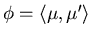 согласованы, если согласованы, если
-
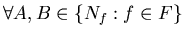 справедливо справедливо
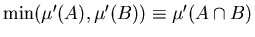 , ,
-
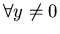 справедливо справедливо 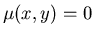 , ,
-
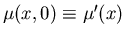 . .
Скажем, что базовое множество предикатов 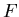 и основание
и основание
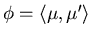 вырождены,
если для любого отношения вырождены,
если для любого отношения
![$\rho\subseteq[0,1]^2$](images/igmd/img61.gif) , любой ЗИП , любой ЗИП
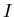 типа типа
![$\langle [0,1],[0,1],\rho \rangle$](images/igmd/img82.gif) и
любого ИГ и
любого ИГ
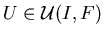 выполняется выполняется
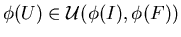 . .
Теорема 3
Базовое множество предикатов 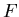
и основание
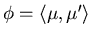 вырождены,
тогда и только тогда, когда они согласованы.
- 1
-
Гасанов Э. Э. Информационно-графовая модель
хранения и поиска данных.
Интеллектуальные системы (1998) 3, 3-4,
163-192.
- 2
-
Гасанов Э. Э. Об одной математической модели
информационного поиска.
Дискретная математика (1991) 3, 2, 69-76.
- Работа выполнена при финансовой поддержке
Российского фонда фундаментальных исследований
(грант 98-01-00130)
Труды IV Международной конференции по математическому моделированию, Москва (27 июня – 4 июля 2000 г.), – том II, Из-во "Станкин", Москва, 2001.
Наверх
|