|
Сотрудники :: Гасанов Эльяр Эльдарович :: Публикации Гасанова Э.Э.
К вопросу о предикатной эквивалентности формул алгебры логики
Гасанов Э.Э., Шакиров А.А.
Кафедра математической теории интеллектуальных систем,
механико-математический факультет МГУ им М.В.Ломоносова
Пусть 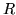 и и 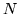 – множества действительных и натуральных чисел,
соответственно; – множества действительных и натуральных чисел,
соответственно;
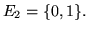
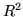 – двумерное евклидово пространство и – двумерное евклидово пространство и
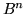 – единичный – единичный 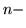 мерный куб. мерный куб.
Пусть
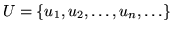 и и
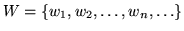 – алфавиты переменных
принимающих значения из – алфавиты переменных
принимающих значения из 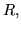 и из и из 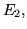 соответственно.
Далее для простоты
вместо соответственно.
Далее для простоты
вместо 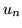 и и 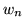 будем использовать знаки будем использовать знаки 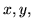 и и
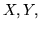 соответственно, возможно, с индексами. соответственно, возможно, с индексами.
Пусть
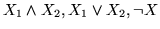 суть булевы функции,
называемые,
соответственно, конъюнкцией, дизъюнкцией и отрицанием и суть булевы функции,
называемые,
соответственно, конъюнкцией, дизъюнкцией и отрицанием и  –
множество этих функций. –
множество этих функций.
Обычным образом введем понятие формулы над 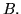
Пусть 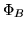 – множество всех формул над – множество всех формул над 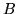 и
и
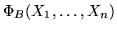 (или просто (или просто
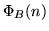 ) – множество
всех формул над ) – множество
всех формул над 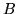 , реализующих функции, существенно зависящие
от переменных , реализующих функции, существенно зависящие
от переменных
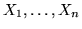 . .
Формулы 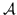 и и 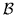 из из 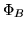 называются равными, если они реализуют
равные функции. Это отношение равенства
разбивает
называются равными, если они реализуют
равные функции. Это отношение равенства
разбивает 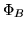 на классы эквивалентности на классы эквивалентности 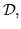 которые содержат точно все формулы, которые реализуют равные функции.
которые содержат точно все формулы, которые реализуют равные функции.
Открытое множество в 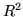 будем называть также областью
или фигурой. будем называть также областью
или фигурой.
Рассмотрим множество базисных фигур в 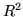
 Каждой фигуре
Каждой фигуре  сопоставим предикат сопоставим предикат 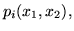 областью истинности которого является
областью истинности которого является 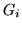 , ,
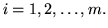
Пусть
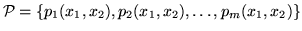 и и
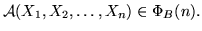 Подставим в
Подставим в 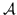 вместо каждой
переменной вместо каждой
переменной 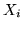 предикат предикат 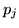 из из 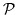 .
Данную операцию назовем полной подстановкой (или просто подстановкой),
и полученное выражение .
Данную операцию назовем полной подстановкой (или просто подстановкой),
и полученное выражение
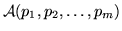 назовем назовем 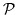 -формулой. -формулой.
Поскольку описания фигуры 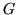 как в виде открытого подмножество
плоскости, так и в виде предиката как в виде открытого подмножество
плоскости, так и в виде предиката  , область истинности которого есть
это подмножество , область истинности которого есть
это подмножество 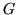 , являются тавтологичными, то мы далее
будем использовать предикат , являются тавтологичными, то мы далее
будем использовать предикат  для обозначения фигуры для обозначения фигуры 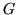 и будем говорить "фигура
и будем говорить "фигура  " несмотря на то, что " несмотря на то, что  –
предикат, описывающий фигуру –
предикат, описывающий фигуру 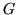 . .
Каждая 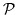 -формула -формула
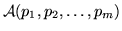 задает некий предикат, или что то же самое
некую фигуру.
задает некий предикат, или что то же самое
некую фигуру.
Фигуры 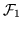 и и 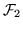 называются равными (пишем
называются равными (пишем
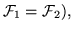 если они совпадают в
если они совпадают в 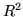 как множества. как множества.
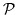 -формулы -формулы
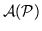 и и
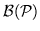 назовем назовем
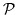 -равными
(пишем -равными
(пишем
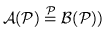 ,
если они задают равные фигуры. ,
если они задают равные фигуры.
Пусть 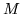 – некоторое подмножество
множества всех – некоторое подмножество
множества всех 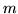 -подстановок -подстановок 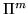 . .
Формулы 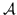 и и 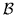 называются называются 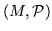 -равными,
(пишем -равными,
(пишем
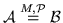 ),
если при любой соответственно одинаковой подстановке ),
если при любой соответственно одинаковой подстановке 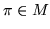 в них предикатов из
в них предикатов из 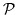 вместо переменных
получаемые вместо переменных
получаемые 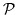 -формулы являются -формулы являются
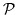 -равными. -равными.
Отношение 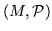 -равенства
на множестве -равенства
на множестве 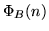 разбивает
это множество на классы эквивалентности разбивает
это множество на классы эквивалентности
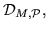 которые содержат точно все такие формулы, которые являются
которые содержат точно все такие формулы, которые являются
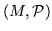 -равными. -равными.
Будем говорить, что множество базисных фигур 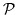 обладает
обладает 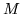 -свойством, если отношения равенства булевских формул
и -свойством, если отношения равенства булевских формул
и 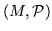 -равенства эквивалентны, т. е.
разбиения -равенства эквивалентны, т. е.
разбиения 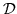 и и
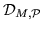 совпадают,
или, что то же самое,
для любых двух формул совпадают,
или, что то же самое,
для любых двух формул
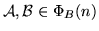 верно
верно
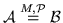 тогда и только тогда, когда
тогда и только тогда, когда
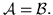
Множество всех граничных точек фигуры  назовем границей назовем границей
 фигуры фигуры 
Не имеющую самопересечений замкнутую ломаную, состоящую из
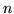 отрезков, назовем отрезков, назовем
 угольником. угольником.
Область в 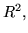 граница которой является граница которой является 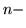 угольником, называется угольником, называется
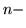 угольной областью.
Заметим, что для любого невырожденного угольной областью.
Заметим, что для любого невырожденного 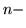 угольника
существует две угольника
существует две 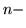 угольные области, границей которых он
является (внешняя и внутренняя). угольные области, границей которых он
является (внешняя и внутренняя).
Если  некоторая фигура, то обозначим некоторая фигура, то обозначим
Пусть  – некоторая фигура. Через – некоторая фигура. Через 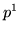 обозначим фигуру обозначим фигуру  ,
а через ,
а через 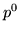 – дополнение к фигуре – дополнение к фигуре  , т.е. фигуру , т.е. фигуру
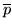 . .
Пусть
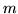 -подстановка из -подстановка из 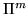 и и
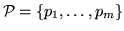 –
множество базисных фигур.
Тогда булевскую функцию –
множество базисных фигур.
Тогда булевскую функцию
назовем определяющей функцией множества базисных фигур
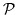 относительно подстановки относительно подстановки 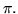
Пусть
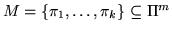 и и
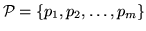 – множество базисных фигур,
тогда булевскую функцию – множество базисных фигур,
тогда булевскую функцию
назовем определяющей функцией множества базисных фигур
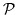 относительно множества подстановок относительно множества подстановок 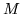 . .
Теорема 1
Пусть
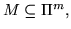 тогда
множество базисных фигур
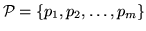
обладает 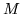 -свойством
тогда и только
тогда, когда
Теорема 2
Для любого 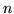 из 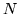
если
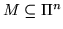 и
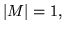 то
существует такое множество базисных фигур
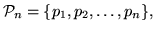
обладающее 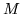 -свойством, что для каждого
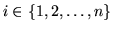
фигура 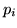 является
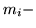 угольной областью, где
Теорема 3
Для любого 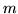 из 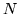 существует такое число 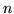 в 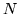 , что
если
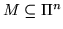 и
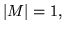 то
никакое
множество базисных фигур
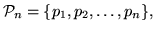
где при
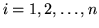
каждая область 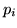 является 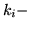 угольной и 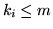 ,
не может обладать 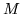 -свойством.
Обозначим через 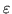 следующую подстановку следующую подстановку
Теорема 4
Для любого 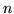 из 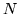 и произвольного множества базисных фигур
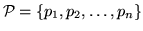 справедливо
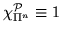 тогда и только тогда, когда
на каждом слое куба 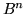 существует хотя бы один набор
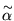 такой, что
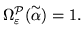
Теорема 5
Для любого 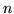 из 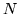 и произвольного множества базисных фигур
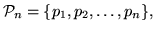 такого, что
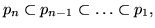
справедливо, что 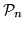 обладает 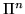 -свойством.
Труды II Международной конференции "Дискретные модели в теории управляющих систем", Красновидово, (23–28 июня 1997 г.), – М: Диалог-МГУ, 1997,
Наверх
|