Предлагается модификация алгоритма Бентли-Маурера, решающего
двумерную задачу интервального поиска. Эта модификация
позволяет снизить исходное логарифмическое среднее время
поиска до константного при сохранении логарифмического
времени поиска в худшем случае. При этом этот алгоритм
зависит от параметра, при вариации которого объем памяти,
необходимый алгоритму, изменяется от
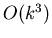
до
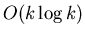
,
при этом среднее время поиска (без учета времени на
перечисление ответа) изменяется от
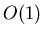
до
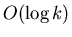
.
В частности, для любого
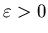
при объеме памяти
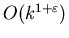
достигается среднее время поиска
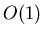
. На основе этих результатов
получены верхние оценки
функциональной сложности двумерной задачи интервального
поиска.