|
Сотрудники :: Носов Валентин Александрович :: Публикации Носова В.А.
О построении классов латинских квадратов в булевой базе данных.
Носов В.А.
Кафедра Математической теории интеллектуальных систем
В работе предлагается конструкция
параметрических классов латинских квадратов размером 2n´2n
над множеством булевских векторов длины n, которая не требует
запоминания латинского квадрата. Дается один классификационный результат для
выполнения данной конструкции.
1) Напомним, что латинский квадрат над
множеством S есть таблица размером n´n,
где n = ½S½, из элементов множества S,
в каждой строке и в каждом столбце которой все элементы различны. Латинские
квадраты широко используются в теории кодирования, планирования эксперимента,
связи в секретных системах ([3], [4], [5]). В настоящее время имеются различные
способы построения латинских квадратов, в том числе и с использованием алгебраических
структур на множестве S. Однако, все эти способы
предполагают, чтобы соответствующий латинский квадрат запоминался целиком, что
затрудняет использование их в случае больших S.
Целью настоящей работы является конструкция параметрических классов латинских
квадратов в булевской базе данных, т.е. для случая S
= En – множество булевских векторов длины n.
При этом будем предполагать, что латинский квадрат не запоминается целиком, а
определяется локальным образом с помощью функций, задающих по номеру строки и
столбца значение соответствующего элемента в латинском квадрате. Другой
рассмотренный вопрос – конструкция параметрического класса латинских квадратов,
в которых при любом значении параметра эффективно определяется номер строки по
любому номеру столбца и элементу этого столбца. В данной конструкции это
осуществляется на тех же функциях, которые определяют латинский квадрат.
Приведен один классификационный результат, связанный с реализацией данной
конструкции.
2) Пусть En – множество двоичных наборов длины n.
В этом случае латинский квадрат над множеством En может быть задан системой из n
булевых функций
f1(x1, …, xn, y1, …, yn) (1)
f2(x1, …, xn, y1,
…, yn)
…
fn(x1, …, xn, y1,
…, yn)
от 2n
переменных, где x1, …, xn определяет номер строки, y1, …, yn – номер столбца, значения функций f1, …, fn определяют соответствующий элемент квадрата.
Используя результаты о регулярности
системы булевых функций [7], можно доказать
Утверждение I.
Система n булевых функций f1, …, fn от 2n переменных x1, …, xn, y1, …, yn определяет латинский квадрат тогда и только тогда, когда во
всех произведениях fi1…fik, 1 £ i1 < … < ik £ n, k
< n в полиноме Жегалкина нет членов, содержащих вхождения x1…xn либо y1…yn, а произведение f1…fn содержит оба таких члена и не содержит других членов, их
содержащих.
Данное утверждение не дает эффективного
способа построения нужных систем булевых функций, однако позволяет
сформулировать ряд достаточных условий, путем рассмотрения классов используемых
функций.
3) Предложим теперь способ введения параметра
в семейство латинских квадратов.
Пусть дано
семейство булевых функций g = (g1(z1,
…, zn), …, gn(z1, …, zn)) от n переменных z1, …, zn. (2)
Пусть p1
(x1, y1), …, pn(xn, yn) – система булевых функций
от 2-х переменных.
(3)
Определим систему булевых функций f1, …, fn от 2n переменных x1, …, xn, y1, …, yn соотношениями:
f1 = x1 + y1
+ g1(p1 (x1, y1), …, pn(xn, yn)) (4)
f2 = x2 + y2
+ g2(p1 (x1, y1), …, pn(xn, yn))
…
fn = xn + yn
+ gn(p1 (x1, y1), …, pn(xn, yn))
Напомним (см.
[1 ]), что семейство булевых функций g = (g1, …, gn)
называют правильным, если для любых различных наборов переменных 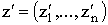 и и 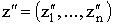 существует a
Î существует a
Î
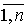 такое, что выполнено такое, что выполнено
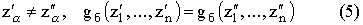
Утверждение
2. Система булевых функций f1, …, fn
вида (4) определяет латинский квадрат для любых функций двух переменных p1,
…, pn в том и только в том
случае, когда семейство функций g
= (g1, …, gn) является
правильным.
Пусть существуют функции p1,
…, pn от двух переменных,
такие, что семейство f1,
…, fn,
определенное (4), не определяет латинский квадрат. Тогда
f1(x’1,
…, x’n, y1, …, yn) = f1(x”1,
…, x”n, y1, …, yn) (6)
…
fn(x’1, …, x’n,
y1, …, yn) = fn(x”1, …, x”n,
y1, …, yn)
для некоторых x’1, …, x’n, x”1, …x”n, y1, …, yn, причем (x’1, …, x’n) ¹
(x”1, …, x”n), либо
f1(x1, …, xn,
y’1, …, y’n) = f1(x1, …, xn,
y”1, …, y”n) (7)
…
fn(x1, …, xn,
y’1, …, y’n) = fn(x1, …, xn,
y”1, …, y”n)
для некоторых x1, …, xn, y’1, …y’n, y”1,
…, y”n, причем (y’1,
…, y’n) ¹
(y”1, …, y”n).
Пусть выполнено (6), тогда используя (4) получаем, что
x’1 + g1(p1 (x’1, y1), …, pn(x’n, yn)) = x”1
+ g1(p1 (x”1, y1), …, pn(x”n, yn)) (8)
…
x’n + gn(p1 (x’1, y1), …, pn(x’n, yn)) = x”n
+ gn(p1 (x”1, y1), …, pn(x”n, yn))
Введем обозначения
z’ = (z’1, …, z’n), где z’i = pi(x’i, yi), i = 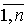
z” = (z”1, …, z”n),
где z”i
= pi(x”i, yi), i = 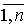
Рассмотрим
пару наборов
g(z’) = (g1(z’), …, gn(z’))
и g(z”) =
(g1(z”), …, gn(z”)).
Если для всех a
Î
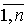 выполнено ga(z’) ¹ ga(z”), то условие правильности семейства функций g1, …, gn не выполняется на паре
наборов z’ и z”. Если существует a
Î выполнено ga(z’) ¹ ga(z”), то условие правильности семейства функций g1, …, gn не выполняется на паре
наборов z’ и z”. Если существует a
Î
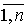 , такое, что выполнено ga(z’) = ga(z”), то из (8) получаем, что x’a
= x”a
и поэтому pa(x'a,
ya)
= pa(x”a,
ya)
и, следовательно, z’a
= z”a.
Значит, в этом случае также не выполняется условие правильности семейства g1, …, gn на паре z’, z”. Случай (7) разбирается аналогично.
Таким образом, если система функций (4) не определяет латинский квадрат при
некоторых функциях p1, …, pn, то семейство g1, …, gn
не является правильным. , такое, что выполнено ga(z’) = ga(z”), то из (8) получаем, что x’a
= x”a
и поэтому pa(x'a,
ya)
= pa(x”a,
ya)
и, следовательно, z’a
= z”a.
Значит, в этом случае также не выполняется условие правильности семейства g1, …, gn на паре z’, z”. Случай (7) разбирается аналогично.
Таким образом, если система функций (4) не определяет латинский квадрат при
некоторых функциях p1, …, pn, то семейство g1, …, gn
не является правильным.
Пусть теперь семейство g1, …, gn не является
правильным. Это значит, что существует пара наборов z’ = (z’1, …, z’n)
и z” = (z”1, …, z”n), что для всех a
Î
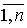 с условием z’a
¹
z”a
имеем ga(z’) ¹ ga(z”). Рассмотрим произвольные x1, …, xn
и y1, …, yn. Определим пару
x’1, …, x’n и x”1, …, x”n, где с условием z’a
¹
z”a
имеем ga(z’) ¹ ga(z”). Рассмотрим произвольные x1, …, xn
и y1, …, yn. Определим пару
x’1, …, x’n и x”1, …, x”n, где
x’i = xi + gi(z’), i Î 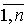 (9) (9)
x”i = xi +
gi(z”), i Î 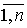
Теперь
определим функции p1,
…, pn так, чтобы
pi(x’i, yi) = z’i,
i Î 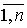 (10) (10)
pi(x”i,
yi) = z”i, i Î 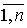
Этого нельзя сделать лишь в случае, когда x’i = x”i, но z’i ¹
z”i для некоторого i Î 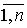 . Но если x’i = x”i, то из (9) имеем gi(z’) = gi(z”) и согласно условия на выбор z’ и z” имеем z’i = z”i. Теперь нетрудно видеть, из (4),
что элементы квадрата, соответствующие (x’1, …, x’n,
y1, …, yn) и (x”1, …, x”n, y1, …, yn) равны (x1, …, xn), т.е. квадрат (4) не
является латинским при данных функциях p1,
…, pn. . Но если x’i = x”i, то из (9) имеем gi(z’) = gi(z”) и согласно условия на выбор z’ и z” имеем z’i = z”i. Теперь нетрудно видеть, из (4),
что элементы квадрата, соответствующие (x’1, …, x’n,
y1, …, yn) и (x”1, …, x”n, y1, …, yn) равны (x1, …, xn), т.е. квадрат (4) не
является латинским при данных функциях p1,
…, pn.
Заметим, что понятие правильности семейства функций было введено в [1]
в связи с изучением регулярности определенного класса булевских автоматов. Там
же приведен критерий правильности и доказана NP-полнота задачи проверки
правильности семейства булевых функций, заданного в КНФ.
4) Введем понятие равномерной обратимости латинского квадрата. Пусть g = (g1, …, gn) – правильное семейство
булевых функций, p1(x1, y1), p2(x2, y2),
…, pn(xn,
yn) –
произвольная функция 2-х переменных. Тогда согласно предыдущему – таблица над En, в которой в
строке x1,
…, xn и в
столбце y1,
…, yn
находится x’1,
…, x’n, где
x’1 = x1 + y1
+ g1(p1 (x1, y1), …, pn(xn, yn)) (11)
…
x’n = xn + yn
+ gn(p1 (x1, y1), …, pn(xn, yn))
будет
латинским квадратом для всех функций p1,
…, pn.
Будем называть
данный латинский квадрат равномерно обратимым и семейство g = (g1, …, gn) также равно обратимым,
если из (11) следует
x1 = x’1 + y1
+ g1(p1 (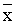 ’1 + y1, y1), …, pn( ’1 + y1, y1), …, pn(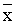 ’n + yn, yn)) (12) ’n + yn, yn)) (12)
…
xn = x’n + yn
+ gn(p1 (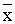 ’1 + y1, y1), …, pn( ’1 + y1, y1), …, pn(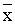 ’n + yn, yn)) ’n + yn, yn))
p1, …, pn, x’1, …, x’n, y1,
…, yn.
Смысл равномерной обратимости заключается в том, что
номер строки произвольного элемента определяется по номеру столбца и значению
элемента с помощью тех же функций g1, …, gn,
p1,
…, pn, которые участвуют в
задании латинского квадрата.
Ограничимся рассмотрением правильных семейств
функций g
вида
g1 = 1, g2
= g2(z1), …, gn = gn(z1,
…, zn-1) (13)
Будем говорить, что семейство
булевых функций (13) удовлетворяет свойству W, если для любого i Î
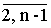 и любого решения z*1, …, z*i-1 уравнения и любого решения z*1, …, z*i-1 уравнения
gi(z1, …, zi-1)
= 0 (14)
справедливо:
функция gj(z*1, …, z*i-1, zi, …, zj-1) не зависит
от zi для
любого j > i.
Утверждение
3. Семейство функций (g1, …, gn)
вида (13) равномерно обратимо тогда и только тогда, когда для него выполнено
условие W.
Пусть условие W выполнено для семейства g. Покажем, что из (11)
следует (12). Доказываем индукцией по n. Для n
= 2 имеем
x’1 = x1 + y1
+ 1
x’2 = x2 + y2
+ g2(p1(x1, y1))
Отсюда
x1 = x’1 + y1
+ 1
x2 = x’2 + y2
+ g1(p1 (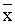 ’1 + y1, y1)) ’1 + y1, y1))
и утверждение
справедливо.
Пусть для n-1 утверждение доказано.
Имеем для xn
соотношение из (11)
xn = x’n + yn
+ gn(p1 (x1, y1), …, pn-1(xn-1, yn-1)) (15)
причем
x1 = x’1 + y1 + 1
x2 = x’2 + y2
+ g2(p1 (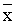 ’1 + y1, y1)) ’1 + y1, y1))
…
xn-1 = x’n-1 + yn-1
+ gn-1(p1 (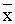 ’1 + y1, y1), …, pn-2( ’1 + y1, y1), …, pn-2(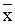 ’n-2 + yn-2, yn-2)) ’n-2 + yn-2, yn-2))
по
предположению индукции.
Нужно
доказать, что
xn = x’n + yn + gn(p1
(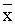 ’1 + y1, y1),
…, pn-1( ’1 + y1, y1),
…, pn-1(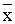 ’n-1
+ yn-1,
yn-1)) (16) ’n-1
+ yn-1,
yn-1)) (16)
В соотношениях (15) и (16) у функции gn значения первых
аргументов совпадают в силу x’1
= x1 + y1 + 1. Далее,
если g2(p1(x1, y1)) = 1, то в
(15) и (16) значения вторых аргументов совпадают у функции gn. Если g2(p1(x1, y1)) = 0, то в
силу свойства W,
функция gn
не зависит от второго аргумента при данной фиксации первого аргумента и, не
меняя значения gn,
мы можем положить в качестве значения второго аргумента p2(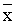 ’2 + y2, y2).
Продолжая таким образом, получаем, что соотношения (15) и (16) совпадают. ’2 + y2, y2).
Продолжая таким образом, получаем, что соотношения (15) и (16) совпадают.
Пусть условие W не выполнено для функции g1, …, gn.
Значит, существует набор z1,
…, zn такой,
что для некоторого i Î 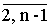 выполнено выполнено
gi(z1, …, zi-1)
= 0
но gj(z1, …, zi, …, zj-1) ¹
gj(z1, …, 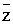 i,
…zj-1)
для некоторого j > i. Рассмотрим произвольное x1, …, xn И y1 = y2
= … = yn =
0. Определим функции p1, …, pn так, чтобы i,
…zj-1)
для некоторого j > i. Рассмотрим произвольное x1, …, xn И y1 = y2
= … = yn =
0. Определим функции p1, …, pn так, чтобы
p1(x1, y1) = z1, p2(x2, y2) = z2,
…, pn(xn, yn) = zn.
Пусть x’i = xi + yi
+ gi(p1 (x1, y1), …, pn(xn, yn)), i = 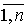 . .
Теперь положим
p1(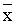 ’1, y1) = z1, p2( ’1, y1) = z1, p2(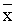 ’2, y2) = z2, …, pi( ’2, y2) = z2, …, pi(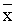 ’i, yi) = ’i, yi) = 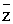 i, …, pn( i, …, pn(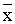 ’n, yn) = zn. ’n, yn) = zn.
Это можно
сделать, так как равенство xi = 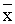 ’i
влечет gi =
1, что противоречит выбору z1, …, zn. ’i
влечет gi =
1, что противоречит выбору z1, …, zn.
Теперь ясно, что для (11) не выполняется (12)
при данном g1, …, gn,
p1,
…, pn на индексе j.
Свойство W позволяет строить
конкретные равномерно обратимые семейства g1, …, gn.
Например,
g1 = 1, gi+1 = gi×zi, i = 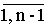 , g1 = 1, gi+1 = , g1 = 1, gi+1 = 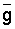 i×zi, i = i×zi, i = 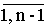 . .
6о.
Для реализации предложенной конструкции латинских квадратов представляют
интерес классификационные результаты для правильных семейств булевых функций. Заметим,
что семейство функций 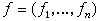 , для которого граф , для которого граф 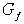 существенной зависимости переменных не имеет циклов, является
правильным. Обратное, как не трудно проверить, не является верным . существенной зависимости переменных не имеет циклов, является
правильным. Обратное, как не трудно проверить, не является верным .
Рассмотрим класс мультиаффинных функций 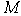 . Напомним, что булева функция . Напомним, что булева функция 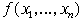 называется
мультиаффинной, если она представляется в виде конъюнкции линейных функций. называется
мультиаффинной, если она представляется в виде конъюнкции линейных функций.
Пусть
семейство 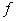 состоит из
мультиаффинных функций. Это значит, что состоит из
мультиаффинных функций. Это значит, что 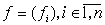 имеет вид имеет вид
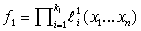
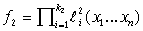
... (17)
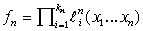
где
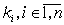 – число перемножаемых
линейных функций в – число перемножаемых
линейных функций в 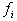 , , 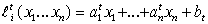 – линейная функция
над – линейная функция
над 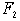 , , 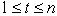 . .
Определим
ориентированный граф 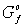 вхождения переменных
в семейство вхождения переменных
в семейство 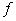 , полагая , полагая 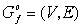 , где , где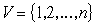 . .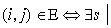 функция
функция 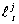 содержит содержит 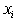 (т.е. (т.е. 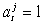 ). (18) ). (18)
Заметим,
что граф 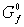 вхождения переменных
содержит в качестве подграфа граф вхождения переменных
содержит в качестве подграфа граф 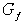 существенной
зависимости переменных семейства существенной
зависимости переменных семейства 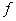 . Построение графа . Построение графа 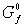 просто, построение
графа просто, построение
графа 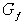 представляет собой
нетривиальную задачу. Для многих классов функций установлена NP-трудность
задачи проверки существенности переменного ([2]). представляет собой
нетривиальную задачу. Для многих классов функций установлена NP-трудность
задачи проверки существенности переменного ([2]).
Простым
элементарным циклом орграфа 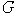 будем называть цикл,
никакое собственное подмножество вершин которого не образует цикл. будем называть цикл,
никакое собственное подмножество вершин которого не образует цикл.
Утверждение
4
Семейство мультиаффинных булевых функций 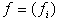 , , 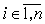 является правильным
тогда и только тогда, когда для любого простого элементарного цикла является правильным
тогда и только тогда, когда для любого простого элементарного цикла 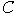 графа вхождения графа вхождения 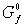 семейства семейства  выполнено условие выполнено условие
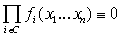 (19) (19)
Пусть
существует простой элементарный цикл 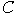 графа графа 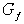 , такой, что условие (19) не выполнено, т.е. , такой, что условие (19) не выполнено, т.е.
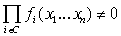 (20) (20)
Для
определенности пусть 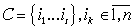 . Это значит, что функция . Это значит, что функция 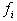 содержит вхождение
переменной содержит вхождение
переменной 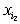 и не содержит
вхождения переменных и не содержит
вхождения переменных 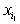 , , 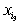 , ..., , ..., 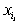 . .
Аналогичное
высказывание справедливо о функциях 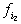 , ..., , ..., 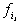 . Представим функции . Представим функции 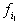 , ..., , ..., 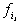 в виде в виде
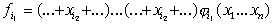
... (21)
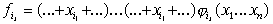
Здесь
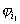 – мультиаффинная
функция, не содержащая вхождений – мультиаффинная
функция, не содержащая вхождений 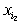 . Сомножители у . Сомножители у 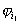 отвечают линейным
функциям, содержащим вхождение отвечают линейным
функциям, содержащим вхождение 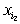 . Аналогично, . Аналогично, 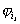 – мультиаффинная
функция, не содержащая вхождений – мультиаффинная
функция, не содержащая вхождений 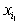 , сомножители у , сомножители у 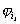 отвечают линейным
функциям, содержащим вхождение отвечают линейным
функциям, содержащим вхождение 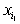 . .
Согласно (20) существует двоичный набор
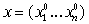 , такой, что , такой, что 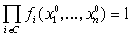 . .
Следовательно имеем
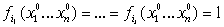 (22). (22).
Рассмотрим двоичный набор 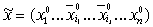 , полученный из , полученный из 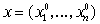 отрицанием переменных
с индексами из отрицанием переменных
с индексами из 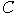 . .
Тогда на основании (21) получаем, что
на данном наборе выполнено
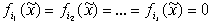 (23). (23).
Из соотношений (22) и (23) следует, что
семейство 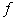 не является
правильным, т.е. для него не выполнено условие правильности на наборах не является
правильным, т.е. для него не выполнено условие правильности на наборах 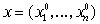 и и 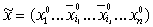 . Обратно, пусть теперь для любого простого элементарного
цикла . Обратно, пусть теперь для любого простого элементарного
цикла 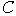 графа графа 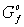 выполнено условие
(19). выполнено условие
(19).
Для семейства 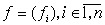 рассмотрим семейство
функций рассмотрим семейство
функций 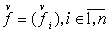 , положив , положив
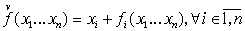 (24). (24).
Пусть 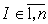 – множество индексов, – множество индексов,
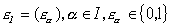 – семейство констант.
Для произвольной функции – семейство констант.
Для произвольной функции 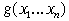 положим положим
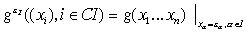
т.е.
переменные с индексами из 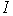 замещены константами замещены константами 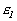 , , 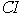 – дополнение – дополнение 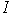 в в 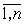 . Известно (см.[1], лемма 2), что . Известно (см.[1], лемма 2), что 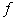 правильное семейство
в том и только в том случае, когда семейство правильное семейство
в том и только в том случае, когда семейство 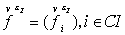 регулярно при всех регулярно при всех 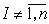 и всех и всех 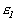 . Для установления регулярности произвольного семейства
булевых функций . Для установления регулярности произвольного семейства
булевых функций 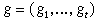 от переменных от переменных 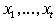 будем пользоваться
критерием Хаффмена (см. [6]), согласно которому семейство будем пользоваться
критерием Хаффмена (см. [6]), согласно которому семейство 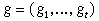 регулярно тогда и
только тогда, когда для любых индексов регулярно тогда и
только тогда, когда для любых индексов 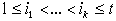 произведение произведение 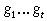 не содержит члена не содержит члена 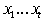 в полиноме Жегалкина
при в полиноме Жегалкина
при 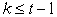 , а произведение , а произведение 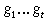 содержит такой член.
Пусть I=ш. Покажем регулярность семейства содержит такой член.
Пусть I=ш. Покажем регулярность семейства 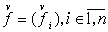 . .
Имеем
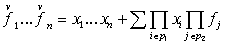 (25). (25).
Суммирование по всем разбиениям 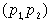 множества множества 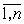 , где , где 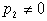 . Покажем, что . Покажем, что 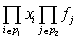 при любых при любых 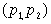 , , 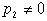 не содержит члена не содержит члена 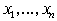 . Если, напротив, для некоторого . Если, напротив, для некоторого 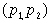 , , 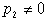 имеется член x1x2…xn , то выполнено имеется член x1x2…xn , то выполнено 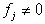 при при 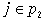 и и 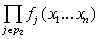 содержит член содержит член 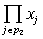 . .
Рассмотрим подграф 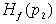 графа графа 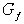 , содержащий вершины множества , содержащий вершины множества 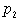 . Из предыдущего следует, что из каждой вершины выходит по
крайней мере одна дуга. Легко видеть, что в этом случае . Из предыдущего следует, что из каждой вершины выходит по
крайней мере одна дуга. Легко видеть, что в этом случае 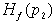 содержит простой
элементарный цикл содержит простой
элементарный цикл 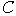 и тогда по условию
должно быть и тогда по условию
должно быть 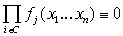 . Но . Но 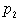 содержит вершины содержит вершины 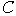 в качестве
подмножества. Тогда в качестве
подмножества. Тогда 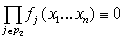 . Значит, член . Значит, член 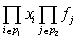 при при 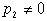 не содержит члена не содержит члена 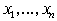 и, следовательно, по (25)
произведение и, следовательно, по (25)
произведение 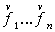 содержит такой член. содержит такой член.
Пусть теперь существует 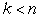 и индексы и индексы 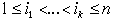 , что произведение , что произведение 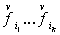 содержит член содержит член 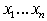 . .
Имеем
 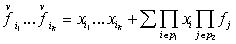 (26). (26).
Суммирование по всем разбиениям 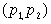 , , 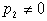 множества i1, i2 ,…,ik
. Это значит, что существует (р1,р2), р2?0, такое, что множества i1, i2 ,…,ik
. Это значит, что существует (р1,р2), р2?0, такое, что 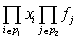 содержит член содержит член 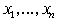 . Отсюда следует, . Отсюда следует, 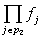 содержит член содержит член 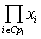 , где , где 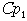 – дополнение
множества – дополнение
множества 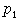 в в 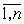 . Рассмотрим подграф . Рассмотрим подграф 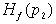 с вершинами
множества с вершинами
множества 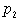 . Поскольку функции с
индексами из . Поскольку функции с
индексами из 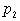 дают член дают член 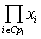 , то по определению графа , то по определению графа 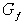 из каждой
вершины из каждой
вершины 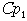 выходит по крайней
мере одна дуга с концом в выходит по крайней
мере одна дуга с концом в 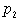 . По условию имеем . По условию имеем 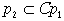 . Следовательно, граф . Следовательно, граф 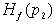 содержит цикл,
поэтому, аналогично предыдущему, имеем содержит цикл,
поэтому, аналогично предыдущему, имеем 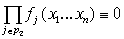 и член и член 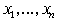 появиться в (26) не
может. Таким образом, появиться в (26) не
может. Таким образом, 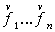 – регулярное семейство согласно критерия
Хаффмена. – регулярное семейство согласно критерия
Хаффмена.
Пусть 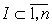 – собственное
подмножество, – собственное
подмножество, 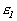 – произвольное
семейство констант. Регулярность семейства – произвольное
семейство констант. Регулярность семейства 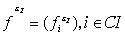 (от переменных (от переменных 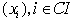 ) устанавливается повторением предыдущих рассуждений. Это
возможно потому, что при замещении переменных константами мультиаффинная
функция остается мультиаффинной и условие (19) также сохраняется при замене
переменных константами. Тем самым утверждение доказано. ) устанавливается повторением предыдущих рассуждений. Это
возможно потому, что при замещении переменных константами мультиаффинная
функция остается мультиаффинной и условие (19) также сохраняется при замене
переменных константами. Тем самым утверждение доказано.
Литература.
[1].
Носов В.А. Критерий регулярности булевского неавтономного автомата с
разделенным входом. Интеллектуальные Системы, т. 3, вып. 3-4, 1998, с. 269-280.
[2].
Алексеев В.Б., Носов В.А. NP-полные задачи и их
полиномиальные варианты. Обзор. Обозрение промышленной и прикладной математики,
1997, т. 4, вып. 2, с.165-193.
[3].
Белоусов В.Д., Белявская Г.Б. Латинские квадраты, квазигруппы и их приложения.
Кишинев, 1989, 80 с.
[4].
Шеннон К. Теория связи в секретных системах. В сб. К. Шеннон. Работы по теории
информации и кибернетике, М., 1963, с.333-369.
[5]. Denes J., Keedwell A.D. Latin
squares and their applications, Budapest, 1974, 547 p.
[6]. Huffman D.A. Canonical forms
for information lossless finite-state logical machines. IRE Trans. Circ. Theory, 1959, v.6, p.41-59.
[7].
Клосс Б.М., Мальшев В.А. Oпределениe
регулярности автомата по его каноническим уравнениям. Докл. АН СССР. 1967. т.
172, №3, с.543-546.
Интеллектуальные системы, т.4,вып.3-4, 1999 г.
Наверх
|