Представление функций Pk формулами специального вида
1.1 Доказать следующие соотношения:
1) x 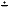 (x (x 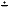 y) = min(x,y) (показать решение) y) = min(x,y) (показать решение)
2)
x 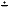 y = x – min(x,y) y = x – min(x,y)
3) (~x) 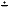 (y (y 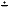 x) = ~ max(x,y) x) = ~ max(x,y)
4)
x 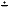 y = max(x,y)-y y = max(x,y)-y
5)
max((x+2) 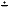 1, Jк-2(x)) = x+1 1, Jк-2(x)) = x+1
6)
max(x+1,y) = max(x,y) + j0(y 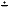 x) + jk-1(x)∙y x) + jk-1(x)∙y
где:
x 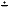 y = x-y, если x>y, 0 иначе y = x-y, если x>y, 0 иначе
~x = (k-1) – x
1.2
Представить функцию Jк-2 в виде суперпозиции функций k-1, x+2 и x 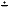 y. y.
1.3
Для заданного k представить функцию f в первой и второй формах:
1)
f = ~x, k=5
2)
f = J0(x2 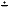 x), k=6,7 x), k=6,7
3)
f = min(x,y), k=3
1.4
Доказать, что при составном k функция f не представима
многочленом:
1) f = ji(x) (показать
решение)
2)
f = x 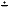 y y
3)
f = max(x,y)
1.5
Привести пример функции из P4, существенно зависящей от 2 переменных, принимающих
только значения 0 и 2 и не представимой в виде многочлена
Список задач по Pk
|