Исследование систем функций k-значной логики на полноту
3.1
Выяснить, полны ли в Pк следующие системы:
1) { 1, J0(x), J2(x), min(x,y), max(x,y) }, k=3 (показать
решение)
2)
{ 1, 2, J2(x), min(x,y), max(x,y) }, k=3
3)
{ 1, 2, J0(x), J1(x), min(x,y), max(x,y) }, k=4
3.2
Используя метод сведения к заведомо полным системам, доказать
полноту:
1) { 1, x2-y, min(x,y) } (показать
решение)
2)
{ k-1, x 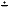 y, x+y } y, x+y }
3)
{ 1, 2x+y, x2 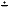 y } y }
3.3
Используя критерий Слупецкого, доказать полноту:
1)
{ k-1, j0(x), x+y }
2) { j2(x), x+y2, x∙y+1 } (показать решение)
3.4
Исследовать на полноту следующие системы:
1) { k-2, x+y, min(x,y) } (показать решение)
2) { 1, 2, x 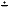 y +1 } y +1 }
3) { 2 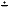 x, max(x,y), x∙y } (показать
решение) x, max(x,y), x∙y } (показать
решение)
4) { ~x, 2j0(x), J1(x), x 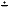 y } y }
3.5
Подсчитать число существенных функций в Pк, зависящих от переменных x1,... xn.
3.6
Доказать, что каждый замкнутый класс в Pк имеет не более чем счетное
множество предполных в нем классов.
Список задач по Pk
|