Программа кандидатского минимума по специальности 01.01.09 (дискрентая математика и математическая кибернетика – интеллектуальные системы)

Распознавание образов

1)      Задача распознавания образов. Основные подходы: геометрический, вероятностный и комбинаторно-логический. Примеры задач распознавания.

2)      Геометрический подход. Линейные процедуры распознавания. Перцептроны. Теорема Новикова. Метод потенциальных функций.

3)      Вероятностный подход. Процедура Байеса. Метод обобщенного портрета. Условия кластеризации. Основные процедуры построения кластеров. Метод скрытых марковских процессов.

4)      Комбинаторно-логический подход. Линейные процедуры и информационные веса. Условия эффективности распознавания. Тесовые процедуры распознавания. Алгоритм голосования. Оценки длины минимальных тестов.

5)      Оценки числа тупиковых тестов для почти всех таблиц. Асимптотически оптимальный алгоритм построения множества коротких тестов. Полиномиальный характер решающих правил распознавания.

Базы данных

1)      Основные модели данных: иерархическая, сетевая, реляционная, дедуктивная.

2)      Основные структуры данных: списки, сортирующие деревья, 2-3-деревья, В-деревья.

3)      Информационно-графовая модель данных. Критерий допустимости информационных графов. Критерий полноты базового множества. Сложность. Мощностная нижняя оценка.

4)      Задачи поиска с коротким ответом. Древовидность оптимальных информационных графов для задач поиска с коротким ответом. Нижняя оценка сложности задач поиска с коротким ответом в случае равновероятных теней записей.

5)      Задача поиска идентичных объектов. Константный в среднем алгоритм поиска идентичных объектов. Оценки памяти константного в худшем случае алгоритма поиска идентичных объектов.

6)      Задача включающего поиска. Нижняя оценка сложности включающего поиска. асимптотическая неулучшаемость нижней оценки. Нижняя оценка сложности в классе древовидных схем.

7)      Одномерная задача интервального поиска. Оценки сложности одномерного интервального поиска при вариации базового множества. Мгновенное решение одномерной задачи интервального поиска.

Решатели задач

1)      Язык логики высказываний. Алгоритм распознавания выполнимости и общезначимости формул логики высказываний: алгоритм Куайна, алгоритм Девиса-Патнема; алгоритм, основанный на правиле резолюции.

2)      Язык логики предикатов. Аксиоматические системы. Предваренная и сколемовская нормальные формы, для формул логики предикатов.

3)      Теорема Эрбрана.

4)      Алгоритм унификации и правило резолюции. Теорема о достаточности правил резолюции и склеивания для доказательства теорем логики предикатов.

5)      Принципы управление логическим выводом при доказательстве теорем с помощью резолюции. Линейный вывод. Совместное применение стратегий использования подслучаев и слияния. С-упорядочение. Правила гиперрезолюции и парамодуляции.

6)      Принцип резолюции и алгоритмический язык Пролог. Организация программы и основные принципы программирования на языке Пролог.

Логические функции

1)      Булевские функции. Теорема Поста.

2)      Функции к-значной логики. Теорема Кузнецова.

3)      Теоремы Янова и Мучника.

4)      Теорема Жегалкина и её обобщения.

5)      Теорема Слупецкого.

Автоматы

1)      Конечный автомат и его обобщения. Ограниченно-детерминированные функции. Эквивалентность автоматов. Диагностические, тестовые и установочные эксперименты с автоматами.

2)      Языки и грамматики. Иерархия Хомского. Распознавание языков автоматами. Теорема Клини. Терема Мак-Нотона.

3)      Структурные автоматы. Полнота и выразимость. Континуальность множества предполных классов. Неразрешимость задачи о полноте. Случай задачи о полноте для функций с задержками. Случай линейных автоматов. Полнота системы одноместных автоматов и булевых функций.

4)      Автоматы в лабиринтах. Отсутствие универсального автомата для задачи обхода лабиринтов.

5)      Однородные структуры. Теорема Мура-Майхилла. Теорема о росте «почти всех» конфигураций. Сложность вычисления булевых операторов в однородных структурах.

6)      Взаимное моделирование однородных структур. Примеры однородных универсальных структур.

Алгоритмы

1)      Машины Тьюринга. Вычислимые функции. Универсальные машины Тьюринга.

2)      Рекурсивные функции: примитивно-рекурсивные и частично-рекурсивные. Представление Клини.

3)      Эквивалентность тезисов Тьюринга и Чёрча.

4)      Сложность алгоритмов. Классы Р и NP. Теорема Кука.

Кодирование

1)      Линейные и циклические коды. Коды БЧХ (Боуза-Чоудхури-Хоквингема). Совершенные коды. Коды Хемминга; двоичный и троичный коды Голея.

2)      Криптосистема Мак-Элайса. Криптосистема RSA, Эль-Гамаля.

Комбинаторика и графы

1)      Теоремы Менгера, Кёнига, Холла и Татта.

2)      Применение методов линейного программирования для задач о максимальном паросочетании и о максимальном потоке.

3)      Теорема Дилуорта, лемма Литтлвуда-Оффорда. Теорема Комлоша о числе вырожденных 0-1-матриц.

4)      Теорема Рамсея.

5)      Теорема Туран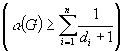а , теорема Эрдёша .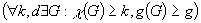

6)      Функция Мёбиуса частично упорядоченного множества. Теорема Холла.

Дискретная оптимизация

1)      Алгоритм построения и минимального остовного дерева.

2)      Построение кратчайших путей в графе. Потоковые алгоритмы.

3)      Рекурсивные алгоритмы и оптимизация (Принцип «Разделяй и властвуй»). Алгоритм Карацубы (Быстрое умножение). Теорема Штрасена (Быстрое умножение матриц)

4)      Градиентные алгоритмы и оптимизация.

5)      Матроиды. Лемма Шпернера. Теорема Дэвэнпорта.

6)      Алгоритмы приближенного решения NP-полных задач: об упаковке в контейнеры, о рюкзаке, о музыкантах, о коммивояжере, о покрытии таблиц.

Литература

К разделу «Распознавание образов»

1)      Кудрявцев В.Б., Алёшин С.В. Дискретные методы распознавания образов, статья в журнале «Интеллектуальные системы».

2)      Дуда Р., Харт П. Распознавание образов и анализ сцен, М., «Мир», 1967 г.

3)      Алешин С.В. Распознавание динамических образов, ч.I. М., издательство МГУ, 1998 г.

4)      Журавлёв Ю.Н. Об алгоритмическом подходе к решению задач распознавания. Проблемы кибернетики, вып.33, М., «Наука», 1978 г.

5)      Константинов Р.М., Королева З.Е., Кудрявцев В.Б., Комбинаторно-логический подход к задачам прогноза рудоносности, Проблемы кибернетики, вып.31, М., «Наука», 1976 г.

6)      Айзерман Н.Н., Браверман Э.М., Розоноер Л.Н., Метод потенциальных функций в теории обучения машин, М., «Наука», 1970 г.

7)      Ту Дж., Гонсалес Р., Принципы распознавания образов., М., «Мир», 1976 г.

К разделу «Базы данных»

1)      Мартин Дж., Организация баз данных в вычислительных системах, Москва, «Мир», 1980 г.

2)      Кнут Д., Искусство программирования для ЭВМ. Москва, «Мир», 1978 г. (том 3, сортировка и поиск).

3)      А Ахо., Дж. Хопкрофт, Дж. Ульман, Построение и анализ вычислительных алгоритмов, Москва, «Мир», 1972 г.

4)      Гасанов Э.Э., Кудрявцев В.Б., Теория хранения и поиска информации. Москва, «Физматлит», 2002 г.

К разделу «Решатели задач»

1)      Э. Мендельсон, Введение в математическую логику. Москва., «Наука», 1971 г.

2)      Ч. Чень, Р. Ли, Математическая логика и автоматическое доказательство теорем.

3)      Э. Хант, Искусственный интеллект, Москва, «Мир», 1978 г.

4)      Дж. Малпас, Реляционный язык Пролог и его применение. Москва, «Наука», 1990 г.

5)      Представление и использование знаний. под. ред. Х. Уэно, М. Исидзука, Москва, «Мир», 1989 г.

6)      Ж.-Д. Лорьер, Системы искусственного интеллекта. Москва, «Наука», 1991 г.

7)      А. Кофман, Введение в прикладную комбинаторику. Москва, «Наука», 1975 г.

8)      Гэри, Джонсон, Вычислительные машины и трудно решаемые задачи. Москва, «Мир», 1982 г.

9)      Дж. Дэвенпорт, И. Сирэ, Э. Турньэ, Компьютерная алгебра. Москва, «Мир», 1991 г.

10)  А.С. Подколзин, Об организации баз, ориентированных на автоматическое решение задач. Дискретная математика, 1991 г., т.3, вып.33, стр.13-30.

11)  Методы компьютерной алгебры, используемые для упрощения выражений и символьного решения алгебраических уравнений.

К разделу «Логические функции»

1)      С.В. Яблонский, Введение в дискретную математику. Москва, «Наука», 1979 г.

2)      С.В. Яблонский, Г.П. Гаврилов, В.Б. Кудрявцев, Функции алгебры логики и Поста. Москва «Наука», 1966 г.

К разделу «Автоматы»

1)      Кудрявцев В.Б., Алёшин С.В., Подколзин А.С., Введение в теорию автоматов. Москва, «Наука», 1985 г.

2)      Кудрявцев В.Б., Функциональные системы. Москва, Изд-во МГУ, 1982 г.

3)      Кудрявцев В.Б., Подколзин А.С., Болотов А.А., Основы теории однородных структур. Москва, «Наука», 1990 г.

К разделу «Теория алгоритмов»

1)      Мальцев А.И., Алгоритм и рекурсивные функции. Москва, «Наука», 1965 г.

2)      Яблонский С.В., Введение в дискретную математику. Москва, «Наука», 1986 г.

3)      Ахо А., Хопкрофт Дж., Ульман Дж., Построение и анализ вычислительных алгоритмов. Москва, «Мир», 1970 г.

4)      Гери М., Джонсон Д., Вычислительные машины и труднорешаемые задачи. Москва, «Мир», 1982 г.

5)      Севидж Джон Э., Сложность вычислений. Москва, «Факториал», 1998 г.

К разделу «Кодирование»

1)      Ф.Дж. Мак-Вильямс, Н.Дж.А. Слоэн, Теория кодов, исправляющих ошибки. Москва, «Связь», 1979 г., 748 стр.

2)      А. Саломаа, Криптография с открытым ключом. Москва, «Мир», 1996 г., 320 стр.

К разделу «Комбинаторика и графы»

1)      О. Оре, Теория графов. Москва «Наука», 1980 г., 336 стр.

2)      Ф. Харари, Теория графов. Москва «Мир», 1973 г., 303 стр.

3)      А. Схрейвер, Теория линейного и целочисленного программирования. Т.1, 2, Москва, «Мир», 1991 г.

4)      Bélla Bollobas Random graphs «Academic press», New York, 1985.

5)      А. Ирматов, Ж.Д. Ковиянич, Об асимптотике логарифма числа пороговых функций к-значной логики. Дискретная математика, т.10, 1998 г., вып 3, стр.35-56.

6)      П Эрдёша, Дж. Спенсер, Вероятностные методы в комбинаторике. Москва «Мир», 1976 г., 132 стр.

7)      Р. Стенли, Перечисленная комбинаторика. Москва «Мир», 1990 г., 440 стр.

К разделу «Дискретная оптимизация»

1)      М. Гери, Д. Джонсон, Вычислительные машины и трудно решаемые задачи. Москва, «Мир», 1982 г.

2)      А. Ахо, Дж. Хопкрофт, Дж. Ульман, Построение и анализ вычислительных алгоритмов. Москва, «Мир», 1979 г.

3)      Форд, Фалкерсон, Потоки в сетях.