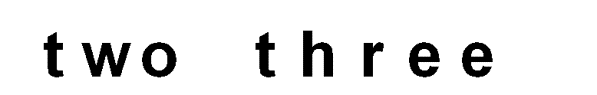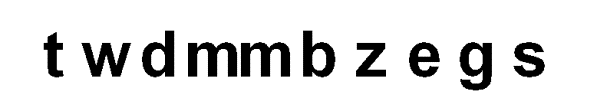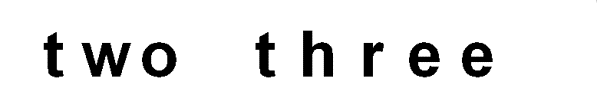Исправление ошибок в формальных языках

А.Б. Холоденко
МГУ им. М.В. Ломоносова, Воробьёвы Горы, Москва, Россия.
Механико-математический факультет, кафедра МаТИС.
e-mail: kholoden@mech.math.msu.su

В работе рассматривается задача автоматического исправления ошибок в распознающих системах; описываются результаты исследований и экспериментов. Приводятся оценки скорости предложенных алгоритмов. Описывается экспериментальная система распознавания печатных текстов.

The problem of automatic error correction in recognizers is considered in this paper; results of investigations and experiments are described. The assessments of offered algorithms' speed are shown. Experimental computer system for printed text recognition is described.

Введение.

При построении распознающих систем зачастую концентрируются на создании универсального алгоритма, на который и возлагается вся ответственность за точность распознавания. Очевидно, однако, что усовершенствование универсального распознающего алгоритма, хотя и улучшит точность распознавания, но все же не сможет обеспечить абсолютной точности. Использование же дополнительной информации об объекте распознавания позволяет даже для не очень точных алгоритмов существенно снизить процент ошибок.

Рассмотрим для примера процесс распознавания печатного текста, введенного в компьютер при помощи сканера. При обычном подходе распознающая программа пытается сначала выделить буквы, а затем – при помощи каких-либо методов распознать их. Однако в случае сильного зашумления текста или наличия каких-либо дефектов распознавание отдельных букв станет невозможным или сильно затрудненным. Их появление, скорее всего, приведет к ошибкам в распознавании. Однако в том случае, если мы знаем, что вводимый текст является осмысленным текстом на некотором языке, от этих ошибок можно попытаться избавиться.

Договоримся называть распознающую программу базовой распознающей системой, а дополнительный модуль, отвечающий за правильность получаемой на выходе информации – корректором.

Необходимые определения.

Всюду далее под алфавитом мы будем понимать конечное множество символов, под цепочкой – конечную последовательность символов алфавита. Словарем назовем некоторое подмножество цепочек, про которые будем говорить, что они являются правильными словами языка. Грамматикой назовем конечную совокупность правил, позволяющую формально определить, является ли данная последовательность правильных слов правильным предложением языка.

Введем еще несколько понятий.

Обобщенной цепочкой над алфавитом A будем называть ориентированный граф без ориентированных циклов, каждому ребру которого приписан символ алфавита и неотрицательное целое число, называемое штрафом. Длинной обобщенной цепочки назовем количество вершин в ее графе. Вершину, в которую не входит ни одного ребра, назовем начальной вершиной, а вершину, из которой не выходит ни одного ребра, назовем конечной. Очевидно, что каждая обобщенная цепочка содержит по крайней мере одну начальную и одну конечную вершину. Без ограничения общности в нашей задаче можно считать, что каждая обобщенная цепочка содержит в точности одну начальную и одну конечную вершину.

Для улучшения качества распознавания базовая распознающая система может выдавать на выходе не один вариант распознавания, а набор вариантов, представленных  в виде обобщенной цепочки. В том случае, если базовая распознающая система не может выдать набор вариантов, обобщенную цепочку можно получить, сопоставив каждому символу a множество символов S(a), которые могут быть перепутаны с a и построив для каждого ребра столько параллельных ребер, какова мощность множества S(a).  

Формальная постановка задачи.

Сформулируем теперь решаемую задачу.

Зафиксируем словарь и грамматику. Требуется проверить, существует ли в данной обобщенной цепочке путь, идущий из начальной вершины в конечную и обладающий следующими условиями:

1. Существует разбиение этого пути на правильные слова из словаря.

2. Полученное разбиение является правильным предложением языка.

В том случае, если хотя бы один такой путь существует, требуется предъявить один путь или все пути, удовлетворяющие вышеприведенным условиям.

Результаты исследований.

В результате проведенных исследований были построены алгоритмы, позволяющие решать предложенную задачу в том случае, если словарь и грамматика могут быть описаны при помощи регулярных или контекстно-свободных грамматик. Оказалось, что решение этих задач может быть проведено последовательно, то есть сначала можно отобрать только те пути, которые допускают разбиение на правильные слова. В этом случае на выходе алгоритма коррекции будет получена обобщенная цепочка над алфавитом всех правильных слов (или классов слов). Эту цепочку затем можно подать на вход корректора следующего уровня.

В результате анализа предложенных алгоритмов были доказаны теоремы, устанавливающие оценки их сложности. В сводном виде эти оценки приводятся в таблицах 1 и 2 (число n означает длину обобщенной цепочки). Константы здесь зависят от словаря и мощности алфавита.

В таблице 1 приведены оценки скорости предложенных алгоритмов для случая регулярных грамматик.

Таблица Таблица 1. Случай регулярных грамматик.

Следует отметить, что в случае конечного словаря оценки могут быть понижены. Так, например, в этом случае задача нахождения одного пути для случая словарного контроля может быть решена за линейное время.

В таблице 2 приведены оценки скорости алгоритмов для случая контекстно-свободных грамматик.

Таблица 2. Случай контекстно-свободных грамматик.

Эксперименты.

Для оценки применимости предложенных методов на практике была создана экспериментальная компьютерная система распознавания, имитирующая распознавание введенных сканером текстов. Графический образ текста сильно искажался, а затем проводилось распознавание сначала без помощи корректирующего блока, а затем – с ним.

Распознающая система реализована в виде программы, написанной на Microsoft Visual C++ 6.0 и работающей в операционных системах Windows 9x и Windows NT версии 4.0 и выше. Система может работать как с предустановленными шрифтами, так и со шрифтами, созданными пользователем. Словарь системы строится при помощи однопроходного алгоритма из задаваемого пользователем текстового файла и в текущей реализации ограничен 5 тысячами слов.

При экспериментах словарь системы состоял из английских числительных от нуля до ста (всего – 28 слов) и нескольких дополнительных слов, таких как, "now", "it", "is" и другие. Общий размер словаря составлял около ста слов. Использовалась тривиальная грамматика (все возможные предложения считались правильными).

На рисунках 1 – 4 показан "протокол" работы программы, то есть результаты основных этапов распознавания.

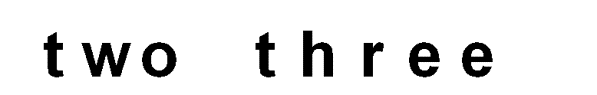
Рисунок Рисунок 1. До искажения.

На первом рисунке приведен исходный графический образ текста, полученного программой.

Рисунок Рисунок 2. Рисунок искажен.

Этот образ текста был сильно зашумлен, чтобы затруднить работу стандартных алгоритмов распознавания. На рисунке 2 показан графический образ текста после зашумления.

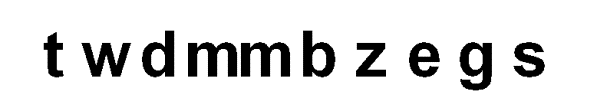
Рисунок 3. Простое распознавание. 

Зашумленный образ был распознан без привлечения информации о словаре. На рисунке 3 приведен результат распознавания. Следует обратить внимание, что всего три символа из восьми были распознаны правильно. Кроме того, был уничтожен пробел между словами и искажена общая длина фразы.

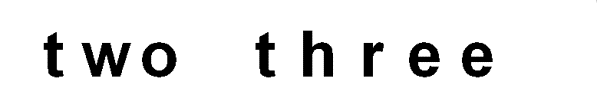
Рисунок 4. Распознавание с корректором. 

На последнем рисунке показан результат распознавания, полученный при применении корректирующего алгоритма. Видно, что текст распознан абсолютно правильно.

Заключение. 

Приведенные результаты теоретических выкладок и практических экспериментов показывают, что предложенный подход может с успехом применяться в распознающих системах, существенно повышая их точность. Примечательно, что метод может применяться не только при распознавании печатных текстов. В настоящее время ведутся эксперименты по использованию этих алгоритмов в задаче распознавания слитной речи.

Литература.

1. А. Ахо, Д. Ульман. Теория синтаксического анализа,  перевода и компиляции. Т.1,2. -М.: Мир, 1978.

2. Кудрявцев В. Б., Алешин С. В., Подколзин A. C. Введение в теорию автоматов. -М.: Наука, 1985.

Материалы конференции "Нейрокомпьютеры и их применение". Москва, 2000 г.