Официальный сайт кафедры Математической теории интеллектуальных систем и лабораторий Проблем теоретической кибернетики и Математичеких проблем искусственного интеллекта механико-математического факультета МГУ им. М. В. Ломоносова

Сотрудники

Сотрудники :: Подколзин Александр Сергеевич :: Публикации Подколзина А.С.

Компьютерное моделирование посредством решения математических задач.

Подколзин А.С.
Учебное пособие по спецкурсу "Компьютерный решатель математических задач" (24 стр.)

Скачать пособие полностью в формате PDF (200 кб): reshatel.zip
Для просмотра Вам понадобится Adobe Acrobat Reader 4.x-5.x
Узнать подробнее о Решателе и познакомиться с его компьютерной версией
можно в отдельном разделе нашего сайта.

Формализация понятия задачи при разработке систем автоматического решения задач часто приводит к необходимости использования логического языка для представления обрабатываемой информации, а также связанной с этим языком формальной дедуктивной системы, определяющей допустимые процессы логического вывода. Возникающие здесь математические модели мы проиллюстрируем на двух типичных примерах – языке и исчислении логики высказываний, а также языке и исчислении логики предикатов.

1. Язык логики высказываний

При задании формального логического языка обычно следуют следующей схеме:

а) Указывается конечный либо бесконечный набор символов, образующих алфавит языка; при описании алфавита могут вводиться те или иные характеристики его символов, в частности определяться разбиения их на подклассы.

б) Вводится индуктивное описание множества правильных выражений языка – конечных последовательностей символов алфавита.

в) Индуктивным образом определяется интерпретация языка (либо множеств допустимых интерпретаций), сопоставляющая каждому выражению языка обозначаемую им функцию, либо объект из некоторой "области интерпретации".

Пункты а) и б) задают синтаксис логического языка, пункт в) – его семантику...

2. Язык логики предикатов.

В случае языка логики предикатов наш алфавит будет состоять из следующих групп символов:

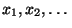
1) Счётный список предметных переменных $x_1,x_2,\dots$

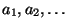
2) Счётный список предметных констант $a_1,a_2,\dots$

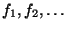
3) Счётный список функциональных символов $f_1,f_2,\dots$

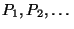
4) Счётный список предикатных символов $P_1,P_2,\dots$

5) Логические константы $\И$ , $\Л$

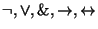
6) Логические связки $\neg,\lor,\&,\rightarrow ,\leftrightarrow$

7) Скобки (,)

Каждый функциональный либо предикатный символ характеризуется своей арностью – некоторым натуральным числом. При этом предполагается, что для каждого натурального 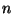имеется бесконечно много как предикатных, так и функциоанальных символов арности ...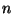

Оглавление

Московский государственный университет

Наверх

Написать вебмастеру

Последние новости - в телеграм-канале кафедры МаТИС:

Компьютерное моделирование посредством решения математических задач.

Подколзин А.С.Учебное пособие по спецкурсу "Компьютерный решатель математических задач" (24 стр.)

Оглавление

Подколзин А.С.
Учебное пособие по спецкурсу "Компьютерный решатель математических задач" (24 стр.)